Funktionsgleichung aus Wertetabelle?
Moin,
ich komme bei einer Mathe-Aufgabe nicht weiter, könnt ihr mir dabei weiter helfen?
Ich möchte anhand einer Wertetabelle (mit 8 Punkten) eine quadratische Funktionsgleichung herausfinden und komme da leider nicht weiter. Wie kann man das am besten machen?
3 Antworten
die Funktion sieht allgemein so aus:
jetzt kannst du also 8 Gleichungen aufstellen (für jeden Punkt eine)...
und dann kannst du mit WolframAlpha a,b,c so bestimmen, dass die Summe der Fehler-Quadrate minimal werden... die zu minimierende Gleichung wär dann:
WolframAlpha kommt auf g(-0.226328, 1.45563, 0.709341)=0.000161174
also liegen wohl nicht alle Punkte voll drauf...
Die Summe der Fehlerquadrate ist bei mir 0.000428343. Da der Wert von Wolfram Alpha besser als meiner ist, muss ich mal mein Verfahren überprüfen.
Das ist aber einigermaßen aufwendig, denn um das exakt zu lösen, müsste man die Gleichung g(a,b,c) nach a, b und c partiell ableiten, die partiellen Ableitungen 0 setzen und das entstehende Gleichungssystem lösen. Das wird wohl heute nichts mehr. Aber es interessiert mich irgendwie, was da los ist.
Da hatte ich mich vertippt. Der y-Wert 3.03 muss 3.05 heißen.
a = -0.22633
b = 1.45563
c = 0.70934
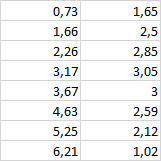
0.73 1.65 1.6513
1.66 2.50 2.5020
2.26 2.85 2.8431
3.17 3.05 3.0494
3.67 3.00 3.0031
4.63 2.59 2.5972
5.25 2.12 2.1132
6.21 1.02 1.0207
Summe der Fehlerquadrate = 0.000161174
Und die Welt ist wieder in Ordnung ;-)
Eigentlich benötigst du nur drei Punkte. Ich würde mir einfach die äußeren und einen mittleren Wert nehmen.
Dann setzt du die Punkte in y = ax² + bx + c ein und löst das Gleichungssystem.
Wenn du so viele Punkte gegeben hast, sollst du wahrscheinlich Punkte wählen, die möglichst wenig vom Verlauf ausreißen oder mehrere Punkte mitteln, sodass der Abstand aller Punkte zur Parabel minimal wird.
Ich habe da etwas mit der Standardabweichung in Erinnerung. Es ist aber zu lange her, dass ich in der Schule war, als dass ich dir das näher erklären könnte.
Du wählst drei Punkte aus der Tabelle, die dir besonders gut gefallen und bastelst daraus drei Gleichungen (LGS).
Dann werden die Unbekannten errechnet (z.B. mit dem Gauß) und schon hast du deine quadratische Funktion.
Ich kommen mit dem gleichen Ansatz auf leicht unterschiedliche Ergebnisse.
Die Punkte liegen aber ganz gut, aber nicht exakt auf der Kurve.