Fünfstellige Primzahlen, Quersumme 13, Querprodukt 28?

Wie finde ich alle fünfstelligen Primzahlen mit QS 13 und Querprodukt 28?

Answer 1

[mihisu]

Das Querprodukt ist 28 = 2² ⋅ 7. Dementsprechend kommt genau eine Ziffer 7 vor, und eine Ziffer 4 oder zwei Ziffern 2. Die restlichen Ziffern sind 1.

Wegen 7 + 4 + 1 + 1 + 1 = 14 kann die Möglichkeit mit Ziffer 4 nicht sein. Demnach müssen die Ziffern 7, 2, 2, 1, 1 sein.

Da nach einer Primzahl gesucht ist, kann keine 2 hinten stehen, da die Zahl sonst durch 2 teilbar wäre.

Es verbleiben dann also erst einmal die folgenden Möglichkeiten:

72211
72121
71221
27211
27121
17221
22711
21721
12721
22171
21271
12271
22117
21217
12217

Wenn man diese Zahlen weiter überprüft, erhält man die folgenden fünfstelligen Primzahlen mit Quersumme 13 und Querprodukt 28 ...

72211
27211
12721
22171

Comments

[mihisu]

Ansonsten könnte man sich auch schnell ein kleines Programm schreiben, dass alle fünfstelligen Zahlen überprüft. Hier ein Beispiel mit Python ...

def isQuer(n):
    qs = 0
    qp = 1
    while n:
        qs += n % 10
        qp *= n % 10
        n = n//10
    if qs == 13 and qp == 28:
        return(True)
    else:
        return(False)

def isPrime(n):
    for i in range(2, int(n**0.5)+1):
        if n % i == 0:
            return(False)
    return(True)

for n in range(10**4, 10**5):
    if isQuer(n) and isPrime(n):
        print(n)

Ausgabe des Programms:

12721
22171
27211
72211

[gfntom]

@mihisu

Bei dir fehlen in der Antwort oben 3 Möglichkeiten:

11227
12127
21127

Davon ist aber keine eine Primzahl.

[mihisu]

@gfntom

Stimmt, die fehlen. Danke.

[Petra150360]

Vielen Dank!

Answer 2

[gfntom]

Tipp:

5-stellige Zahlen mit QS 13 und QP 28 müssen aus den Ziffern 1,1,2,2 7 sein.

Da es sich um Primzahlen handeln muss, kann die Einerstelle nicht 2 sein.

Hift das weiter?

Comments

[Petra150360]

Danke!!

Answer 3

[hypergerd]

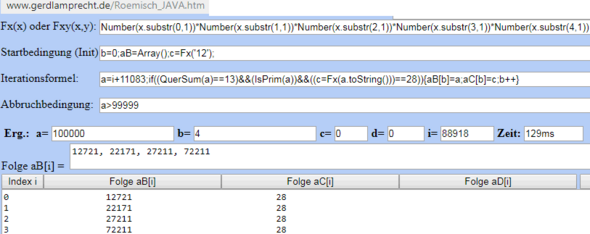
Ich mach's mit dem universellen Iterationsrechner, da mir die vielen Teiler-Gesetzmäßigkeiten zu umständlich sind:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@Ux.substr(0,1))*@Ux.substr(1,1))*@Ux.substr(2,1))*@Ux.substr(3,1))*@Ux.substr(4,1))@Nb=0;aB=Array();c=Fx('12');@Na=i+11083;if((QuerSum(a)==13)&&(IsPrim(a))&&((c=Fx(a.toString()))==28)){@Bb]=a;@Cb]=c;b++}@Na%3E99999@N0@N0@N#

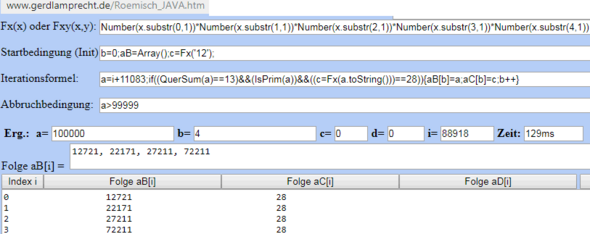
Also 4 Lösungen.

Comments

[Petra150360]

Vielen Dank!

[Petra150360]

Vielen Dank!