Diese Definition sagt einfach aus, dass jedem Element eines Tupels ein Index abgebildet wir oder?

Ich bilde von {1,...,n} zu X ab, also eine natürliche Zahl n erhält ein x € X, also so:

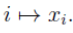
Aber hier steht zu einem n-Tupel (x_1,...,x_n) gehört die Abbildung i |->x_i. Was das bedeutet ist klar, wir haben ein Tupel und jedes Tupel für sich hat hat eine Abildung i |-> x_i, also auf jedes Tupelelement wird ein Index abgebildet, so dass die Elemente im Tupel klar identifiziert werden können und jedes Tupel hat dafür eine eigene Abbildung i |-> x_i. Was mich nur verwirrt, wie soll das gehen?

Wir haben oben stehen: {1,...,n} -> X, also von {1,...,n} zu X, X ist einfach eine Menge mit Elementen und {1,...n} sind natürliche Zahlen also eine natürliche Zahl wird auf ein Element von X abgebildet, hier ist X jedoch ein Tupel bestehend aus einem Element, da X^1?

Answer 1

[DerRoll]

Da steht nicht "jedes Tupel hat eine eigene Abbildung", sondern "jedes n-Tupel hat eine Abbildung von {1, ..., n} nach X". D.h. die Elemente x_1, ..., x_n des n-Tupels induzieren die Abbildung die gerade 1 auf x_1, ..., n auf x_n abbildet. Du liest zu ungenau und denkst immer noch zu kompliziert.

Woher ich das weiß: Studium / Ausbildung – Dipl.Math.

Comments

[kadwin0]

Ohhh, das ist ein großer Unterschied, hast recht! Danke dir. Das

"D.h. die Elemente x_1, ..., x_n des n-Tupels induzieren die Abbildung die gerade 1 auf x_1, ..., n auf x_n abbildet. Du liest zu ungenau und denkst immer noch zu kompliziert."

habe ich so auch verstanden, aber mit dem Unterschied, dass ich verstanden habe, jeder hat eine eigene Abbildung, wenn das nicht der Fall ist, ist das natürlich verständlich, danke dir!