Die Graphen der beiden Funktionen f1 und f2 mit f1(x)=-0,1x²+x und f2(x)=0,5 begrenzen ein Flächenstück.?
Die Graphen der beiden Funktionen f1 und f2 mit f1(x)=-0,1x²+x und f2(x)=0,5 begrenzen ein Flächenstück.?
Bestimme diejenige Parallele zur y-Achse,die aus diesem Flächenstück die längste Strecke herausschneidet.
Ich bin nur zu den Punkten x=5 und y=2,5, welches Flächenstück und welche Parallele?
Danke für Anregungen!
f2(x)=0,5x, habe das x vergessen,sorry!
5 Antworten
So sieht das bildlich aus:
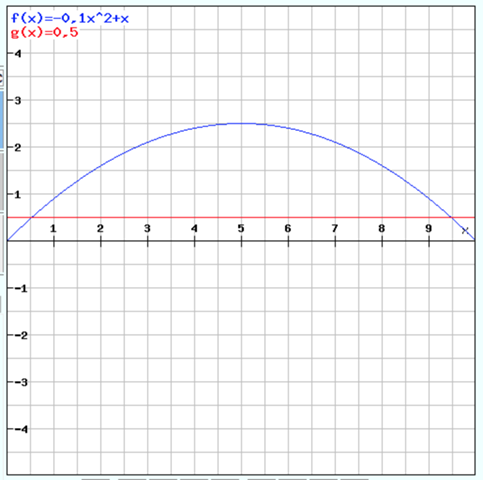
Da müssen wir erstmal die Schnittpunkte von f(x) und g(x) bestimmen:
f(x) = g(x)
-0,1x^2+x = 0,5
-0,1x^2+x - 0,5 = 0
x^2 - 10x + 5 = 0

Die Schnittpunkte iegen also bei x1 = 0,528 und x2 = 9,472
Nun berechnen wir die Fläche A1 unter der Parabel:
F(x) = -1/30 * x^3 + 1/2 x^2
F(0,528) = 0,134
F(9,472) = 16,532
A1 = 16,532 - 0,134 = 16,398
Fläche A2 unter der Geraden:
A2 = (9,472 - 0,528) * 0,5 = 4,472
Eingeschlossene Fläche A:
A = A1 - A2 = 16,398 - 4,472 = 11,926 FE
b) Die Längste Strecke parallel zur y-Achse geht durch den Scheitlepunkt bei x = 5
Da muss man dann einfach rechnen:
f(5) - 0,5 = 2
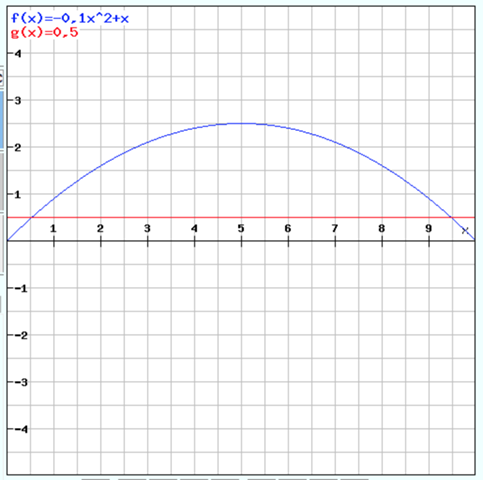

Hallo Hamburger02, ich weiß ich nerve, aber dadurch das f2 ja nun f(x)=0,5x ist ändert sich doch der Graph dafür, weil ich vorher das x vergessen hatte bei f2. Könntest du es nochmal bildlich darstellen.
Danke. Hamburger02, leider habe ich bei f2(x)=0,5 das x vergessen. f2(x)=0,5x,tut mir leid!
Nein, die zwischen dem gelben Kringel und dem grünen Schlunkel.
Was soll denn sonst der Satz "f1 und f2 .... begrenzen ein Flächenstück." wohl bedeuten ??
Hamburger hat ja sogar noch die Funktionsbeschreibung notiert und die jeweiligen Farbe verwendet. Damit der letzt D...kopp es auch erkennen kann.
Ja, bin ich auch sehr dankbar, habe leider einen Fehler von mir entdeckt f2(x(=0,5 x, hatte das x vergessen, sorry!
Was bitteschön ist ein Schlunkel? Wo finde ich den in GeoGebra? ;-)
Die Graphen der beiden Funktionen f1 und f2 mit f1(x)=-0,1x²+x und f2(x)=0,5 begrenzen ein Flächenstück.?
Schnittstellen bestimmen. Über Differenzfunktion in diesem Bereich integrieren.
Bestimme diejenige Parallele zur y-Achse,die aus diesem Flächenstück die längere Strecke herausschneidet.
längere oder längste???
Ich verstehe den Sinn der Aufgabe nicht!
Ist da nicht (ich denke auch mal, dass es "längste" heißen soll) einfach nur die Extremstelle der Differenzfunktion gesucht, also hier die x-Stelle des Scheitelpunkts der Parabel? Also nicht einmal die Fläche...?
Stimme dir zu. Es ist hier ja häufig so, dass nicht einmal die Aufgabenstellung vollständig wiedergegeben werden kann...
So sieht das dann bildlich aus:
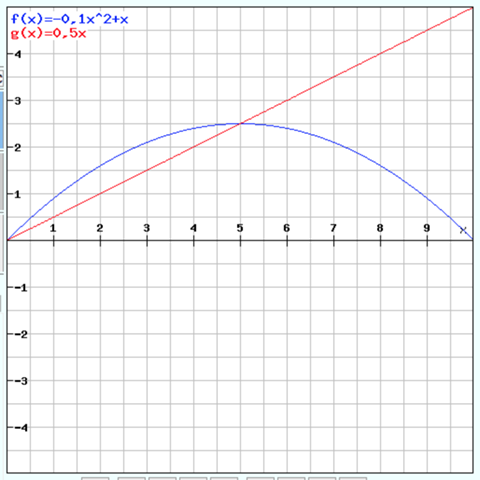
Da müssen wir erstmal die Schnittpunkte von f(x) und g(x) bestimmen:
f(x) = g(x)
-0,1x^2+x = 0,5x
-0,1x^2+x - 0,5x = 0
-0,1x^2 + 0,5x = 0
x^2 - 5x = 0
x(x - 5) = 0
Gemäß dem Satz vom Nullprodukt haben wir damit zwei Lösungen:
x1 = 0
x2 = 5
F(x) = -1/30 * x^3 + 1/2 x^2
F(5) = -1/30 * 125 + 0,5 * 25 = 8,33
F(0) = 0
A1 = 8,33 - 0 = 8,33 FE
Fläche A2 unter der Geraden:
Da gibt es zwei Möglichkeiten
a) Wir berechnen die Dreiecksfläche gemetrisch als Dreieck:
A2 = 1/2 a * h = 0,5 * 5 * 2,5 = 6,25
b) wir integrieren g:
G(x) = 0,25x^2
G(5) = 0,25 * 5^2 = 6,25
Eingeschlossene Fläche A:
A = A1 - A2 = 8,33 - 6,25 = 2,08 FE
b) Die längste senkrechte Strecke zwischen den beiden Funktionen ermitteln wir über eine Maximierung. Dazu setzen wir erstmal die Länge der Strecke s als Differenz zwischen beiden Funktionen an:
s(x) = f(x) - g(x) = -0,1x²+x - 0,5x = -0,1x^2 + 0,5x
s'(x) = -0,2x + 0,5
Maximum bei s'(x) = 0:
-0,2x + 0,5 = 0
0,2x = 0,5
x = 2,5
und damit:
s(2,5) = -0,1(2,5)^2 + 0,5* 2,5 = 0,625
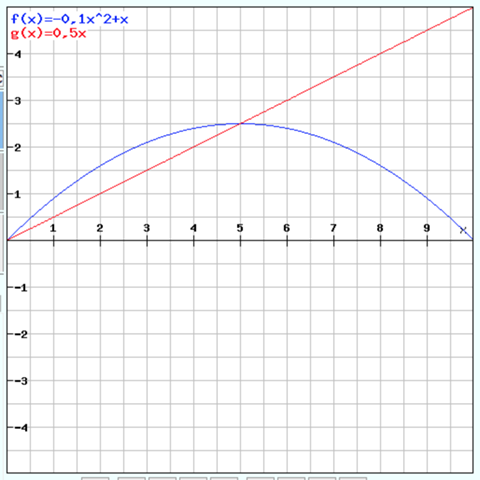
Vielen, vielen Danke für Deine so große Mühe, nun kommt bei mir Licht ins dunkle!!!!!
Was soll "Ich bin nur zu den Punkten x=5 und y=2,5," bedeuten?
Das sind Punkte di mir nix sagen. Du hättest die Schnittstellen der beiden Funktionen bestimmen müssen. Das sind diese beiden aber nicht.
Den Rest hat Wechselfreund bereits skizziert.
Ja, eben die Koordinaten des Scheitelpunktes.
ja, soisses. Habs inzwischen auch gemerkt. dass du diese ausgerechnet hast. Hättest du auch sagen können.
Hast du noch FRagen oder ist inzwischen alles klar?
Ehrlich geschrieben, Nein. Welches Flächenstück ist gemeint? Würde das mal bildlich sehen wollen. Aber , Euch allen sage ich herzlichen Dank !
Klar ist "bildlich sehen" der Schlüssel zur Lösung. Aber das Bild mußt Du dir schon selbst malen.
Koordinatensystem , dann die Gerade f2 und die nach unten offene Parabel f1. Die Fläche dazwischen ist klar und die Parallee zur y-Achse, die am läöngsten ist siehst du auch sofort.
Da müßtest du schon alles erkennen können.
sehe gerade : Hamburger02 hat doch schon alles gezeichnent!!!!!
Warum nutzt du das Bild nicht ?????
Hamburger02 habe ich schon geschrieben und gefragt ob es die Fläche zwischen dem roten und dem blauen Bogen ist ?
Welche denn sonnst? Verstehst du die Skizze denn gar nicht ?
Verstehe ich auch nicht. Die längste Strecke
ist die durch den Scheitelpunkt, und die hast du
ja gefunden. Wie man eine Strecke herausschneidet,
ist mir auch nicht klar.
Danke schön ! Soll die Fläche zwischen dem roten Strich und dem blauen Bogen gemeint sein?