cos, sin, tan ohne Taschenrechner?
Hallo Leute,
Ich muss für eine Arbeit in Mathe bestimmte Winkel im Einheitskreis ausrechnen, jedoch ohne Taschenrechner. D.h, ich bekomme zB den Winkel 90 Grad, und muss sin, cos, tan ohne Taschenrechner ausrechnen. Kann mir jemand behilflich sein und mir erklären wie das funktionieren soll? Gibt es da bestimmte "Formeln" die man eingeben kann und auf das Ergebnis kommt? Danke
3 Antworten
Für bestimmte Winkel wie die Vielfachen von 90° haben Sinus, Cosinus und Tangens besonders einfache Werte. Bei Deinen 90° etwa ist der Cosinus 0, was übrigens auch bei 270° der Fall ist. Der Sinus ist bei 90° gleich 1 und bei 270° gleich –1, und der Tangens ist überhaupt nicht definiert.
Spezielle WinkelEs gibt noch ein paar Winkel wie sin(30°)=cos(60°)=½, bei denen man sich andere Winkel wie –cos(120°)=sin(150°)=½ herleiten kann.
Für Winkel, die ungeradzahlige Vielfache von 45° darstellen, ist der Tangens entweder 1 oder –1 (je nach Quadrant).
Der Sinus und der Cosinus müssen hier beide den Betrag √{½} haben, und Winkel wie cos(30°) oder sin(60°) müssen den Betrag √{¾} haben.
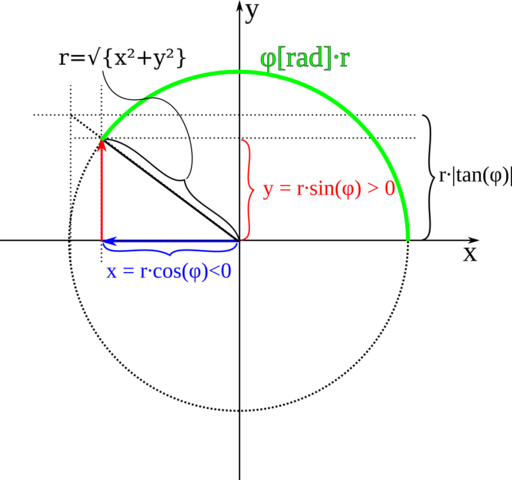
Der Kreis und der Satz des PYTHAGORASDas kannst Du Dir an einem Kreis mit dem Radius r (der beim Einheitskreis gleich 1 ist) verdeutlichen, wobei der feste Winkelschenkel immer die x≥0-Halbgerade bzw. die Strecke zwischen dem Ursprung (0|0) und (1|0) ist.
Der bewegliche Winkelschenkel ist dann eine Halbgerade vom Ursprung aus durch einen Punkt (x|y) auf dem Einheitskreis bzw. die Strecke zwischen (0|0) und (x|y), der mit dem festen Winkelschenkel den Winkel φ bildet.
Diese Strecke ist die Hypotenuse eines rechtwinkligen Dreiecks, dessen Katheten die orthogonalen Projektionen auf die Achsen sind, nämlich
x = r·cos(φ)
y = r·sin(φ)
x/y = tan(φ).
Deshalb ist nach dem Satz des PYTHARGORAS
r = √{x² + x²}
(cos(φ))² + (sin(φ))² ≡ 1.
Wenn Du also den Sinus hast, kannst Du den Cosinus daraus herleiten und umgekehrt.
Primitive pythagoreische TripelBei bestimmten Winkeln übrigens, die leider ziemlich krummzahlig sind, etwa knapp 37°, stehen x,y und r in einem einfachen Verhältnis wie 4:3:5, wie auch übrigens im Schaubild. Die Zahlen 3,4 und 5 bilden ein primitives Pythagoreisches Tripel, was sich aus
3² + 4² = 9 + 16 = 25 = 5²
ergibt.
Winkel im BogenmaßBei sehr kleinen Winkeln φ sind sowohl der Sinus als auch der Tangens nahezu gleich dem Verhältnis des zwischen den Winkelschenkeln liegenden Kreisbogenstücks zu r.
Letzteres ist (immer, nicht nur bei kleinen Winkeln) φ im Bogenmaß, hier jetzt als φ[rad] (Radian) bezeichnet. „Grad“ ist nämlich eine Pseudo-Maßeinheit, auch Hilfsmaßeinheit (s. Wikipedia-Artikel) genannt.
Das trifft eigentlich auch auf den Radian zu, der ja eigentlich auch ein dimensionsloses Verhältnis zwischen zwei Längen ist. Man kann „rad“ auch weglassen.
Das Bogenmaß ist nicht so willkürlich wie das Gradmaß. Dass man den Vollwinkel in 360 Teile teilt, die man „Grad“ nennt, ist historisch bedingt durch das Zahlensystem der antiken Babylonier, in dem die 60 eine große Rolle spielte. Daneben gibt es auch das Gon, den 400. Teil eines Vollwinkels.
Der Vollwinkel im Bogenmaß ist 2π Radian oder einfach 2π (Verhältnis Kreisumfang/r), und daraus ergibt sich
φ[rad] = φ[°]·π/180°
φ[°] = φ[rad]·180°/π.
Ich habe die Zusammenhänge in einem beigefügten Bild zu verdeutlichen versucht.
Schau mal hier :
http://www2.hs-esslingen.de/~kamelzer/2011WS/Werte_sin_cos.pdf
Beim Tangens einfach :
tan(x) = sin(x) / cos(x)
Zig exakte Wurzelwerte und die dazugehörigen Formeln findet man unter
http://lamprechts.de/gerd/sin(x)ExactTrigonometricConstants.htm
Geht weit über das hinaus, was ein Schüler wissen muss.
danke :)