Brauche unbedingt Mathe Hausaufgabe bis MORGEN?
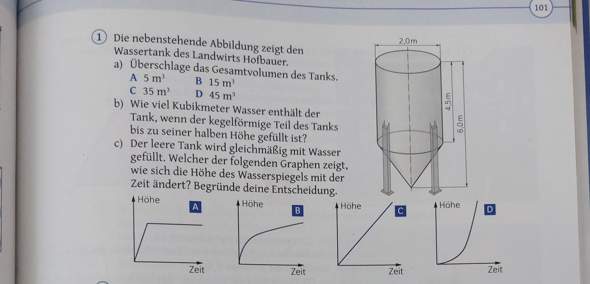
Ich muss morgen Mathe vorstellen und verstehe die 1b und c nicht. Kann mir bitte jemand helfen.
Vielen Dank im Voraus!
3 Antworten
Für Aufgabe 1b musst du zuerst das Volumen des kegelförmigen Teils des Tanks berechnen. Dazu kannst du die Formel für das Volumen eines Kegels verwenden:
Der Radius des Zylinders und des Kegels beträgt 1 Meter,. Das bedeutet, dass die Formel für das Volumen des Kegels
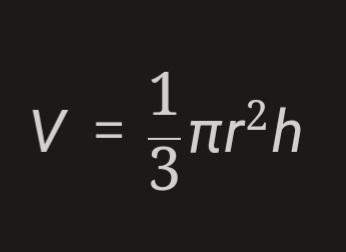
Wenn der Kegel bis zur halben Höhe gefüllt ist, beträgt der Radius des kleinen Kegels 0,5 Meter, wie du richtig gesagt hast. Das Volumen des kleinen Kegels ist dann
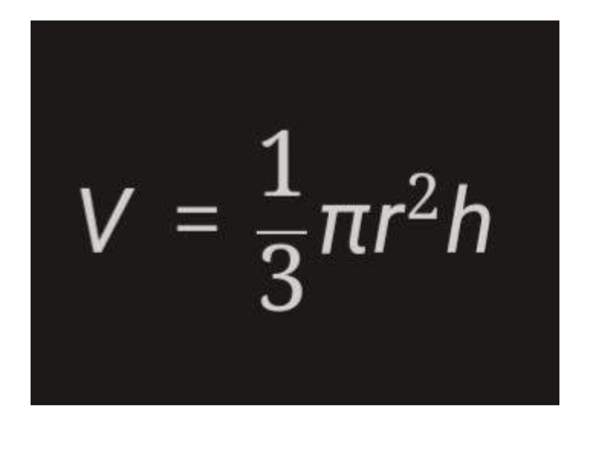
mit r=0,5 m und h=0,75 m. Das Ergebnis ist V=0,196 m³.
Das Volumen des Wassers im kegelförmigen Teil des Tanks ist dann die Differenz zwischen dem Volumen des größeren Kegels und dem Volumen des kleineren Kegels. Ziehe die beiden Volumina voneinander ab und du erhältst das Volumen des Wassers in Kubikmetern:
V= 1,57 - 0,196 = 1,374
Aber mein Mathelehrer hat bei der 1b gemeint das ich das mit dem Vierstreckensatz berechnen kann und ich weiß nicht wie ich den ansetzten soll?
Der Radius des Zylinders und des Kegels beträgt 1 Meter. Wenn der Kegel bis zur halben Höhe gefüllt ist, beträgt der Radius des kleinen Kegels 0,5 Meter.
Das bedeutet, dass die Höhe des Wasserspiegels proportional zur Wurzel aus dem Volumen ist.
Das und die davor stehende Formel ist ebenfalls falsch. Wieso die fehlerhafte Antwort von einem "Experten" bestätigt wurde, ist mir ein Rätsel.
Wenn ich V=⅓πr²•h nach h umstelle, erhalte ich
h=3V/(πr²), also deine Formel ohne Wurzel.
Die Rechnung ist richtig, wenn du das Volumen des kleinen Kegels berechnen willst, der in den großen Kegel passt, wenn der große Kegel bis zur halben Höhe gefüllt ist. Du hast die Formel für das Volumen eines Kegels korrekt angewendet, indem du den Radius und die Höhe des kleinen Kegels eingesetzt hast. Das Ergebnis ist V= 0,196 m³.
Das ist das Volumen des kleinen Kegels, nicht das Volumen des Wassers im kegelförmigen Teil des Tanks. Um das Volumen des Wassers zu berechnen, musst du noch das Volumen des großen Kegels abziehen, das du mit der gleichen Formel berechnen kannst, indem du den Radius und die Höhe des großen Kegels einsetzt. Das Ergebnis ist V = 1,57m³
Das Volumen des Wassers ist dann die Differenz zwischen den beiden Volumina:
V = 1,57 - 0,196 = 1,374
Das ist die richtige Antwort für Aufgabe 1b
V= 1,57 - 0,196 = 1,374
Warum subtrahierst du beide Volumina?
Die obere Teil des Kegels wird doch zuerst gefüllt, da der Kegel auf der Spitze steht.
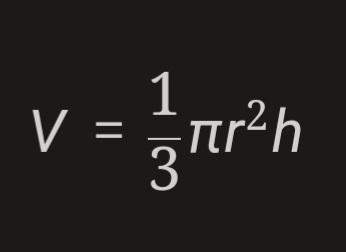
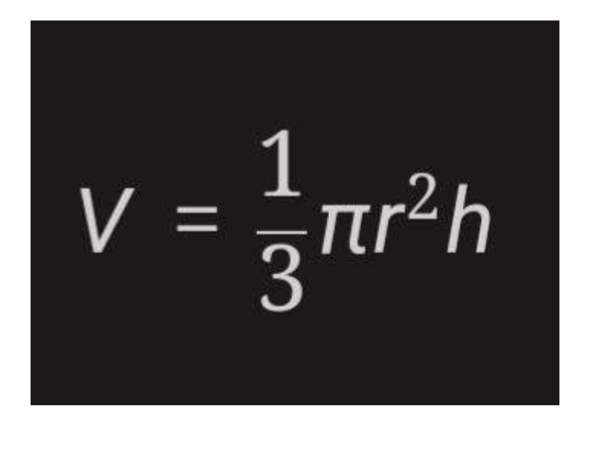
Ich subtrahiere beide Volumina, weil ich das Volumen des Wassers im kegelförmigen Teil des Tanks berechnen will. Das ist die Frage in Aufgabe 1b.
Das Volumen des Wassers ist nicht gleich dem Volumen des Kegels, sondern nur dem Teil des Kegels, der mit Wasser gefüllt ist.
Um diesen Teil zu bestimmen, muss ich das Volumen des leeren Raums abziehen, der sich über dem Wasser befindet.
Dieser leere Raum ist ein kleinerer Kegel, der in den größeren Kegel passt. Deshalb subtrahiere ich das Volumen des kleineren Kegels vom Volumen des größeren Kegels.
das stimmt, dass der obere Teil des Kegels zuerst gefüllt wird, da der Kegel auf der Spitze steht.
Aber das ändert nichts an der Berechnung des Volumens. Egal, ob der Kegel auf der Spitze oder auf der Grundfläche steht, das Volumen des Wassers ist immer gleich dem Volumen des Kegels minus dem Volumen des leeren Raums.
Das kannst du dir auch geometrisch vorstellen, indem du den Kegel umdrehst und den leeren Raum mit Wasser auffüllst. Dann hast du einen vollen Kegel und einen leeren Kegel, die das gleiche Volumen haben wie vorher.
Dieser leere Raum ist ein kleinerer Kegel
Der kleine Kegel ist der mit Wasser gefüllte Raum, dessen Volumen V≈0,196m³ gesucht ist.
Der kleine Kegel ist der mit Wasser gefüllte Raum, dessen Volumen gesucht ist.
Der kleine Kegel ist der leere Raum, der sich über dem Wasser befindet, wenn der große Kegel bis zur halben Höhe gefüllt ist. Der mit Wasser gefüllte Raum ist der Teil des großen Kegels, der unter dem kleinen Kegel liegt.
Der kleine Kegel ist der Teil, der von der horizontalen Linie und den schrägen Linien begrenzt wird. Der mit Wasser gefüllte Raum ist der Teil, der von der Grundfläche und den schrägen Linien begrenzt wird.
Das Volumen des Wassers ist dann die Differenz zwischen dem Volumen des großen Kegels und dem Volumen des kleinen Kegels.
Guck dir noch einmal die Abbildung an. Warum sollte die Spitze des Kegels leer sein, wenn sie zuerst befüllt wird?
Der Kegel ist nicht auf der Spitze stehend, sondern auf der Grundfläche stehend. Das kannst du an der Beschriftung der Höhe sehen, die senkrecht zur Grundfläche ist.
Wenn der Kegel auf der Spitze stehend wäre, wäre die Höhe schräg zur Grundfläche.
Wenn der Kegel auf der Grundfläche stehend ist, wird er von unten nach oben mit Wasser gefüllt. Das bedeutet, dass die Spitze des Kegels leer bleibt, bis der Kegel ganz voll ist.
Das ist der Grund, warum der leere Raum ein kleinerer Kegel ist, der sich über dem Wasser befindet. Das Volumen des Wassers ist dann der Teil des Kegels, der unter dem leeren Raum liegt.
Der Kegel ist nicht auf der Spitze stehend, sondern auf der Grundfläche stehend.
In der Abbildung steht er auf der Spitze.
Wenn der Kegel auf der Spitze stehend wäre, wäre die Höhe schräg zur Grundfläche.
Das ist vollkommen falsch. Die Höhe steht immer senkrecht auf der Grundfläche.
In der Abbildung steht er auf der Spitze.
Das sehe ich, aber die Spitze ist nicht nach unten gerichtet.
Das liegt daran, dass die Abbildung eine perspektivische Darstellung des Kegels ist, die den Eindruck erweckt, dass der Kegel auf der Spitze steht.
Wenn du dir aber die Beschriftung der Höhe anschaust, siehst du, dass sie senkrecht zur Grundfläche ist. Das bedeutet, dass der Kegel auf der Grundfläche steht und die Spitze nach oben zeigt.
Er ist breiter an der Basis und schmaler an der Spitze, was darauf hindeutet, dass der Kegel auf der Grundfläche steht.
Das ist vollkommen falsch. Die Höhe steht immer senkrecht auf der Grundfläche.
Du verwechselst die Höhe mit der Mantellinie. Die Höhe ist die senkrechte Strecke von der Spitze des Kegels zum Mittelpunkt der Grundfläche.
Die Mantellinie ist die schräge Strecke von der Spitze des Kegels zum Rand der Grundfläche. Die Höhe steht immer senkrecht auf der Grundfläche, egal ob der Kegel auf der Spitze oder auf der Grundfläche steht.
Die Mantellinie hingegen ändert sich je nachdem, wie der Kegel steht. Wenn der Kegel auf der Spitze steht, ist die Mantellinie länger als die Höhe. Wenn der Kegel auf der Grundfläche steht, ist die Mantellinie kürzer als die Höhe.
Das kannst du in der Abbildung sehen
Die Höhe ist die Strecke ZA, die senkrecht zur Grundfläche AB ist. Die Mantellinie ist die Strecke ZB, die schräg zur Grundfläche AB ist
Interessant, dass du mir Schulmathematik erklären willst. 😁
Leider enthält dein letzter Kommentar auch wieder Fehler.
Wenn der Kegel auf der Grundfläche steht, ist die Mantellinie kürzer als die Höhe.
Die Mantellinie ist bei einem geraden Kegel immer länger als die Höhe.
Leider siehst du deine Fehler nicht ein. Deshalb ist für mich dieses Thema erledigt.
Welcher letzter Kommentar?
Die Mantellinie ist bei einem geraden Kegel immer länger als die Höhe.
Das ist nicht ganz richtig. Die Mantellinie ist bei einem geraden Kegel immer länger als die Höhe, wenn der Kegel auf der Spitze steht. Wenn der Kegel auf der Grundfläche steht, ist die Mantellinie kürzer als die Höhe.
Das liegt daran, dass die Mantellinie die schräge Strecke von der Spitze des Kegels zum Rand der Grundfläche ist, während die Höhe die senkrechte Strecke von der Spitze des Kegels zum Mittelpunkt der Grundfläche ist. Wenn du den Kegel umdrehst, ändert sich die Länge der Mantellinie nicht, aber die Länge der Höhe schon.
Wenn der Kegel auf der Grundfläche steht, ist die Mantellinie kürzer als die Höhe.
Das ist immer noch falsch.
Wenn du den Kegel umdrehst, ändert sich ... die Länge der Höhe schon.
Nein, die Höhe ändert sich auch nicht.
Wie kommst du auf solche falschen Behauptungen?
Was genau ist falsch? Du musst mir schon erklären was du meinst, ansonsten kann ich dir darauf nicht antworten
Nein, die Höhe ändert sich auch nicht.
Die Höhe ist die senkrechte Strecke von der Spitze des Kegels zum Mittelpunkt der Grundfläche.
Die Mantellinie ist die schräge Strecke von der Spitze des Kegels zum Rand der Grundfläche. Die Höhe steht immer senkrecht auf der Grundfläche, egal ob der Kegel auf der Spitze oder auf der Grundfläche steht. Die Mantellinie hingegen ändert sich je nachdem, wie der Kegel steht. Wenn der Kegel auf der Spitze steht, ist die Mantellinie länger als die Höhe. Wenn der Kegel auf der Grundfläche steht, ist die Mantellinie kürzer als die Höhe. Das kannst du in der Abbildung sehen, die du mir geschickt hast. Die Höhe ist die Strecke ZA, die senkrecht zur Grundfläche AB ist. Die Mantellinie ist die Strecke ZB, die schräg zur Grundfläche AB ist.
Ich habe dir keine Abbildung geschickt.
Für den Radius r, die Höhe h und die Mantellinie s eines geraden Kegels gilt:
s²=r²+h²
Da bei einem Kegel r>0 gilt, ist s>h. Die Mantellinie s ist also immer größer als die Höhe h.
Hallo,
wenn der auf der Spitze stehende Kegel bis zur halben Höhe gefüllt ist, beträgt der Radius auch nur die Hälfte des gesamten Radius.
Das siehst du, wenn du einen Kegel skizzierst und den zweiten Strahlensatz anwendest.
Wenn nun sowohl Radius als auch Höhe halbiert werden, erhält man ein Achtel des Volumens des großen Kegels.
Bei c) kannst du anschaulich argumentieren. Zuerst ist der Radius klein, das Wasser steigt schnell (steiler Kurvenverlauf). Dann wird der Radius größer, das Wasser steigt langsamer (Kurve wird flacher). Schließlich steigt das Wasser gleichmäßig im zylindrischen Abschnitt (linearer, flacher Verlauf).
🤓
Was B Betrifft:
der Kgegelförmige Teil des Tanks ist 1,5 Meter hoch und hat oben einen Durchmesser von 2 Metern. Unten sind es 0 Meter.
Wenn du den kegelförmigen Teil nun bis zur Hälfte füllst, entsteht ein Kegel mit einem großen Durchmesser von einem Meter und einer Höhe von 0,75 Metern.
Mit dieser Formel lässt sich das Volumen eines Kegels berechnen. brauchts noch die Grundlfäche. das wäre
Damit wäre B gelöst....
kommen wir zu C
Da lass uns ein wenig Sherlok holms spielen. was passiert wenn wir gleichmässig schnell Wasser in den tank laufen lassen?
zu nächst mal ist es ja so, dass wir erst den Kegel haben. der fängt klein an und wird immer größer. ab 1,5 m haben wir dann einen Zylonder. ab hier müsste die Höhe gleichmässig steigen von der Geschwindigkleit her.
Damit ist das Weg Zeit Diagramm C schon mal auszuschließen, weil es eine lineare Funktion ist. Das wäre höcshtens für den Abschnitt ab 1,5 m realistisch.
Das Diagramm D da sich der Füllvorgang hier beschleunigt. blieben noch A und B als Lösungen über. die Überlegung ob jetzt A oder B überlasse ich dir. Ich gebe dir aber ein Werkezug an die Hand, dieses Problem zu lösen.
eine Excel Tabelle.
Rechnen wir einfach die Wassermenge im Tank Dezimeter für Dezimeter aus!
in Zelle A1 kommt "Höhe"
Ab Zelle A2 abwärts dann eine Zahlenreihe also 1, 2, 3 4.... bis 45 das wäre dann in Zelle A46
in Zelle B1 kommt "Volumen"
in Zelle B2 dann
=((20/15*A2)^2*PI()/4)*A2/3
Dröseln wir die Formel mal ein wenig auf, das was da hinter der Doppelklammer steht also (20/15*A2) bildet den Duchmesser des Wasserspiegels auf der jeweiligen Höhe in Dezimetern ab.
im weiteren Abschnitt ((20/15*A2)^2*PI()/4) haben wir die Fläche des Wasserspiegels auf der jeweiligen Höhe und last but not least mit der kompletten Formel das Volumen auf der jeweiligen Höhe.
Das Ganze ziehst du einfach bis in Zeile 16, wo also eine 15 davor steht herunter.
Ab der näcshten Zeile brauchts ne neue Formel, weil wir ja ab hier zylindisch sind.
das Volumen eines Zylinders ist Grundfläche mal Höhe. die Grundfläche bleibt eine Konstante. und die Höhe wächst mit.
die zugehörige Formel würde wie folgt lauten:
=20^2*PI()/4*A2+$B$16
dröseln wir das Ganze mal auf....
20^2*PI()/4 ist die Grundfläche in Quadratdezimetern. ab hier bleibt sie ja konstant. mit der Erweiterung 20^2*PI()/4*A2 wird die Höhe des Zylindrischen Teils bestimmt. warum ich damit bei 1 anfange? weil ab hier ja der zylindrische Teil erst einen Dezimeter hoch steht. last but not least mit dem Rest der Foemel wird der kegelige Teil addiert. die Dollarzeichen sind dafür gedacht, dass sich excel beim herunterziehen der Formeln immer wieder auf das Volumen des konischen Teils bezieht,
Ich habe das ans Ende gestellt weil Punkt vor Strich!
nun nennen wir die Spalte C einfach "zeit und sagen einfach es wären 12 Liter pro Minute, die in den Tank fließen. das bedeutet, du teilst einfach den Wert durch 12.
in Salte C2 sollte dann Stehen
=B2/12
Wie das zusammengeht sollte nun klar sein.
Du hast also wie lange es dauert bis die jeweilige Füllhöhe erreicht ist.
wenn du nun ein Liniendiagramm einfügst, solltest du sehen können, welche der vier Linien die richtige ist.
lg, Anna
Ich lese etwas anderes ab.