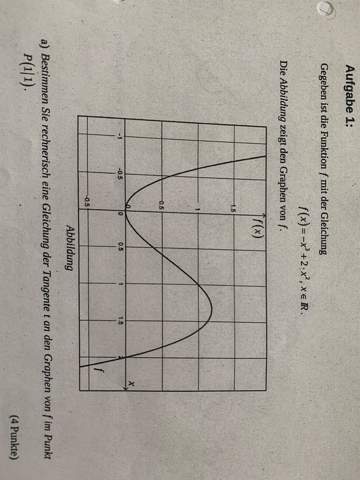
Bestimmen sie rechnerisch eine Gleichung der Tangente t an den Graphen von f im Punkt P (1/1)?
Hallo Zusammen! Ich bin echt schlecht in Mathe und brauche dringend Hilfe zu dieser Aufgabe. Ich habe auch die Lösung dazu, aber ich verstehe die Schritte nicht wie man zum Ergebnis kommt.
hier die Aufgabenstellung:
und hier die Lösung:

Danke schonmal :)
3 Antworten
Die Steigung der Tangente an einem Punkt einer Funktion wird immer durch die erste Ableitung der Funktion beschrieben.
Wenn du also am Punkt 1 die Steigung der Tangente bestimmen willst, musst du die erste Ableitung bilden und für x = 1 einsetzen. Du bekommst dann für y ebenfalls 1 heraus.
Da die Tangente immer eine Gerade ist, wird sie durch eine Geradengleichung beschrieben, die ja die Form y = mx+b hat.
Das m ist die Steigung, die du gerade ausgerechnet hast: 1. Also y = 1x +b.
Das b ist der Schnittpunkt mit der y-Achse. Um b auszurechnen, kannst du den gegeben Punkt (1|1) durch den die Gerade ja gehen muss, einfach als x und y Wert in die Geradengleichung einsetzen: 1 = 1*1 + b. Wenn du das ausrechnest, kommt b=0 heraus und damit hast du die Tangentengleichung: y = x +0 oder y=x
Tangentengleichung yt=ft(x)=f´(xo)*(x-xo)+f(xo)
P(1/1) xo=1 ist die Stelle,wo die Tangente liegen soll
f(x)=-1*x³+2*x² abgeleitet
f´(x)=-3*x²+4*x
f(xo)=f(1)=-1*1³+2*1²=-1+2=1
f´(xo)=f´(1)=-3*1²+4*1=-3+4=1
eingesetzt
ft(x)=1*(x-1)+1=1*x-1+1
yt=ft(x)=1*x=x
hier die Herleitung Tangente- und Normalengleichung,vergrößern und/oder herunterladen


Das ist die Tangentengleichung: y = m*x+b
Du setzt y und x (also von deinem Punkt) ein. Dann stellst du nach b um.
m rechnest du aus, indem du x in die 1. Ableitung einsetzt