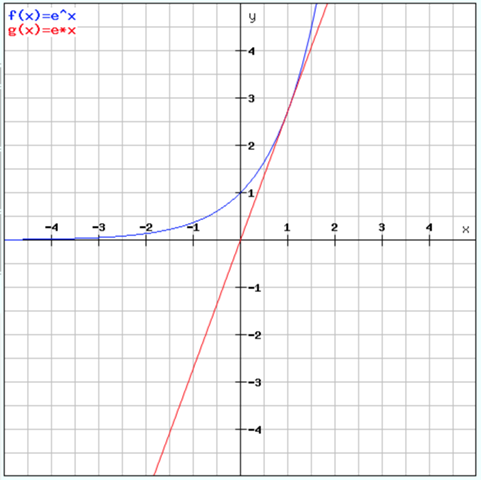
Bestimmen sie rechnerisch die Gleichung der Tangente an den Graphen in P(x0|f(x0)?
Kann mir einer bei 2b) helfen? Ich habe das Gefühl, dass meine Lösung komplett falsch ist.

Was ist denn deine Lösung?
f(1)=e¹
f'(x)=0 --> P(1|0) , m=0
Einsetzen in y=mx+n:
0=0×1+n
0=n --> y=x
Das wäre meine Lösung gewesen aber fühlt sich irgendwie komplett falsch an😅
zeig mal deine Lösung
f(1)=e¹
f'(x)=0 --> P(1|0) , m=0
Einsetzen in y=mx+n:
0=0×1+n
0=n --> y=x
Das wäre meine Lösung gewesen aber fühlt sich irgendwie komplett falsch an😅
4 Antworten
Wir müssen nur die Tangentengleichung berechnen:
Theorie:Tangentengleichung: g(x) = m * x + n
Steigung (m):
Mit m als Steigung der Tangente (Die Steigung der Tangente ist konstant und wir können sie durch die Stelle x_{0} (da wo die Tangente die Funktion f berührt), in der ersten Ableitung von f berechnen.)
1. f(x) ableiten
2. x_{0} in f'(x) einsetzen (f'(x_{0} ) berechnen) -(das Ergebnis ist die Steigung m)
y-Achsenabschnitt (n):
Das n ist der y-Achsenabschnitt der Tangente (Den finden wir heraus wenn wir heraus, indem wir halt den Nullwert mit der y-Achse berechnen. Dafür nehmen wir die einfach schön ausgerechnet Werte der Tangente an x_{0}, setzen sie in die Tangentengleichung ein und stellen nach n um.)
1. x_{0} in f(x) einsetzen (f(x_{0}) berechnen) - (das Ergebnis ist die Berührstelle von Tangente und Funktion f)
2. f(x_{0}) und f'(x_{0}) in die Tangentengleichung einsetzen: f(x_{0}) = f'(x_{0}) * x_{0} - n (f(x_{0}) ist g(x), f'(x_{0}) ist m und x_{0} ist x)
3. Tangentengleichung nach n umstellen (umgestellt: n = f(x_{0}) - f'(x_{0}) * x_{0})
Alles in einer Gleichung:
g(x) = m * x + n
g(x) = f'(x_{0}) * x + f(x_{0}) - f'(x_{0}) * x_{0})
Rechnung:Steigung (m):
1. Ableiten
f(x) = e^{x}
f'(x) = [e^{x}]' | Ableitung der e-Funktion und Kettenregel
f'(x) = [x]' * e^{x} | Potenzregel
f'(x) = 1 * e^{x}
f'(x) = e^{x}
2. x_{0} in f'(x) einsetzen
f'(x) = e^{x}
m = f'(x_{0}) = e^{x_{0}}
m = f'(1) = e^{1}
m = e^{1}
m = e
y-Achsenabschnitt (n):
1. Berechnung der Berührstelle von der Tangente und f
f(x) = e^{x}
f(e^{x_{0}) = e^{x_{0})
f(e^{x_{0}) = e^{1}
f(e^{x_{0}) = e^{1}
f(e^{x_{0}) = e
g(x_{0}) = f(e^{x_{0})
-> g(x_{0}) = e
2. Berechnung von n durch Äquivalenzumformung in einer linearen Gleichung:
g(x) = m * x + n
g(x_{0}) = f'(x_{0}) * x_{0} + n |-(f'(x_{0}) * x_{0})
g(x_{0}) - f'(x_{0}) * x_{0} = n
n = g(x_{0}) - f'(x_{0}) * x_{0}
n = e - e * 1
n = e - e
n = 0
Tangentengleichung:
g(x) = m * x + n
g(x) = e * x + 0
g(x) = e * x
Lösung:
g(x) = e * x
Ich hoffe, dass ich weiterhelfen konnte. ^^
Bei weiteren Fragen stehe ich natürlich zur Verfügung. :3
Die Tangentengleichung ist y = m*x + b
Du musst also m und b herausfinden.
Die Steigung m ist die Ableitung an der Stelle x0, also f'(x0).
b bekommst du, indem du die Gleichung nach b umformst: b = y - m*x
m kennst du ja, x ist x0 und y bekommst du, indem du einfach deinen x-Wert in die Funktion einsetzt.
Am Ende wieder m und b in die Tangentengleichung einsetzen (y und x allgemein lassen)
du hast
P(1 ; e)
f(x)=e^x
f ' (x) = e^x
f ' (1) = e
also m=e
y=mx+b
jetzt m und P einsetzen
e = e • 1 + b
b = 0
dann hast du die Tangentengleichung
y = e • x
ich hab raus:
y = e * x