Bei wie viel Grad erhitzt Wasser am schnellsten?
Mein Mann und ich haben uns heute überlegt, ob es einen Punkt ging, bzw eine Temperatur bei der der Anstieg der Temperatur schneller geht.
Grund: wir haben einen Wasserkocher mit Temperaturvorwahl. Ich kann einstellen bei wieviel grad er stoppen soll und er zeigt an, bei wie viel grad er gerade ist. Ich glaube ja, dass der Wasserkocher das Wasser von 20 auf 60 grad schneller erhitzt hat, als von 50 auf 90.
gibt es nun tatsächlich einen Punkt x wo der Anstieg um die selbe Gradzahl schneller geht? Es müssen ja auch nicht 40 grad sein. Es kann ja auch sein, das 10 grad die perfekte und schnellste Erhöhung sind. Auch beim Ofen halte ich ab und zu um erwärmendes Wasser das terminieret rein und ab 90 grad hab ich manchmal das Gefühl die 10 grad bis es kocht brauchen viel länger als die 10 grad um unser Leitungswasser (sagen wir 18 grad) auf 28 grad zu erhitzen.
Vielleicht gibt es ja Leute die in Physik besser aufgepasst haben, die mir sagen können, wann das Wasser um wie viel grad am schnellsten erhitzt und dazu eine Erklärung liefern kann.
10 Antworten
- In erster Näherung müsste es gleich lange dauern, wenn die Menge, die zugeführte Leistung und der Temp.unterschied gleich sind.
- In zweiter Näherung müsste es bei höherer Temperatur sogar deutlich langsamer gehen, weil es eine exponentielle Erwärmungskurve gibt: Annäherung an die Temperatur des Heizelements, und die Verlustleistung nimmt bei höherer Temp. zu (Wäremeabgabe an die Umgebung):
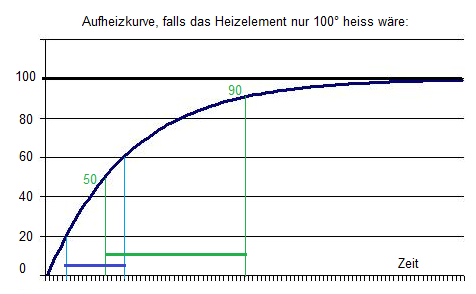
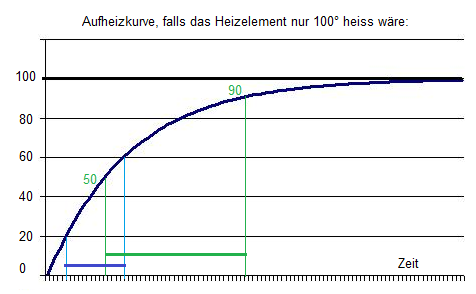
- Weil das Heizelement natürlich viel heisser als 100° ist, wird die Kurve gestreckt, un der Zeitunteschied (blau zu grün, je 40°) wird nicht mehr sooo gross wie aus der Zeichnung abzuleiten wäre.
- Die Temp.-Abhängigkeit der Wärmekapazität spielt hier aber kaum eine Rolle, da sie sich zwischen 20 und 90 Grad nur in wenigen Promillen ändert.
noch zu deiner Frage unten:
"Habe ich in einem anderen Land mit Adapter und meinem eigenen Wasserkocher durch eventuellen Energie Verlust (oder auch nicht?) eine längere warte zeit bis mein Wasser den Siedepunkt erreicht hat?"
Du meinst wohl, wenn du aufgrund einer tieferen Netzspannung mit weniger Leistung heizen kannst?
Ja, dann hast du entsprechend länger, bis das Wasser auf der gewünschten Temperatur ist.
Die "Universalformel" für alle solchen Berechnungen ist:
P * t = 4182 * m * dT
P = Heizleistung in Watt
t = Zeit in Sekunden
m = Masse des Wasser in kg (= ungefähr die Liter)
dT: Temperaturunterschied in Kelvin oder Grad, der erzielt werden muss
(4182 ist die spezifische Wärmekapazität von Wasser in J/kg/K)
Näherungsweise ist der Zusammenhang zwischen Temperatur und zugeführter Energie linear, das gilt aber nur für flüssiges Wasser.
Bei dir wird die infolge eines Temperaturunterschieds vom Wasserkocher an die Umgebung abgegebene Wärme ausschlaggebend sein. Diese hängt vom Temperaturunterschied zwischen Wasserkocher und Umgebung ab, und der ist bei 60 °C Wassertemperatur naturgemäß größer als bei 30 °C.
Bei einem bestimmten Volumen an Wasser bleibt die zugeführte Energie gleich, egal ob du es von 30°C auf 40°C erwärmst oder von 40°C auf 50°C.
Die Wärmekapazität ist nicht ganz konstant.
http://www.wissenschaft-technik-ethik.de/wasser_eigenschaften.html#kap04
Im Bereich zwischen 20 und 50°C ist sie kleiner als im Bereich zwischen 50 und 80°C.
siehe Physik-Formelbuch,was du privat in jedem Buchladen bekommst.
spezifische Wärmekapazität von Wasser c=4,19 KJ/(kg*k)
bedeutet:Man braucht eine Energie von 4,19 KJ (Kilojoule) um 1 kg Wasser um 1° Celsius zu erwärmen
Qzu=m*c*(tw-tk)
Qzu=zugeführte Wärmeenergie in KJ (Kilojoule)
m=Masse des Wassers in kg ,1 Liter Wasser=1 kg Wasser
c=4,19 KJ/(kg*K)
tk=Temperatur des kalten Wassers in Grad Celsius
tw=Temperatur des warmen Wassers in Grad Celsius
Beispielrechnung: m=10 kg tk=10° und tw=40° (Duschtemperatur)
Qzu=10 kg*4,19 KJ/(kg*K)*(40°-10°)
Qzu=1257 KJ
man muss theoretisch eine Energie von Qzu=1257 KJ aufwenden,um 10 kg Wasser von 10° auf 40° zu erwärmen.
Hinweis:Man benötigt natürlich etwas mehr Energie,weil ja auch die Geräte,Topf,Heizplatte ,usw.- miterwärmt werden müssen.
1 KWh(kilowattstunde)=3600 KJ
notwendige elektrische Energie Eel=1257 KJ/(3600 KJ/KWh)=0,349 KWh
Bei einen Preis von 0,28 Euro/KWh wären das 0,349 KWh*0,28 Euro/KWh=0,097 Euro,also etwas über 10 Cent.
Die Heizzeit berechnet sich aus
P=W/t=Qzu/t
t=Qzu/P
Qzu=zugeführte Energie in KJ
P=Heizleistung in KW (Kilowatt) also 1 KW=1000 W (Watt)
Hat das Heizgerät eine Leistung von P=1 KW ergibt sich
t=1257 KJ/1 KW=
t=1257 s (Sekunden)
Hinweis:Rechnerisch hat die Anfangstemperatur keinen Einfluss auf die Heizzeit.
Allerdings fließt bei einem heissen Topf mehr Wärmeenergie an die Umwelt ab.
Ein gut wärmeisolierter Topf ist somit etwas sparsamer,weil dann ja weniger Wärmeenergie an die Umwelt abfließt.
Du gibst dir ja sehr viel Mühe und ist in erster Näherung auch alles richtig, ABER die Wärmekapazität von Wasser (eigtnlich von keiner Substanz) ist über das betrachtete Temperaturintervall nicht ganz konstant.
Hast Recht !
Wenn man absolut präzise nachmessen würde,dann ist c=4,19 KJ/(kg*K) nicht konstant.
Merke:Jede theoretische Berechnung weicht von der Wirklichkeit ab.
Ist diese Abweichung nur 10% oder weniger,so ist die Berechnung brauchbar.
Wenn man mit c=4,19 KJ/(kg*K) rechnet,ist die Genauigkeit im Alltag auf jeden Fall genau.
Genauer ist es,wenn man den Stromzähler abliest.
Man sieht dann genau,was man bezahlen muss.
Beispiel:Flugzeugbau
Man rechnet und rechnet und rechnet und am Schluß macht man Versuche bis zum Bruch des Bauteils,um sicher zu gehen,damit das Bauteil auch wirklich hält.
Die spezifische Wärmekapazität von Wasser ist temperaturabhängig: http://www.wissenschaft-technik-ethik.de/wasser_eigenschaften.html#kap04
Die Abweichung ist aber so gering, dass du das in der Praxis nicht merkst. Was du merkst, ist der Wärmeverlust bei der Erwärmung. Heißt, das Wasser erwärmt sich nur durch Differenz von zugeführter zu verlorener Wärme. Die zugeführte Wärme (Heizleistung) ist praktisch konstant. Der Verlust ist stark Temperaturabhängig. Einmal durch Abstrahlung und Konvektion an der Oberfläche des Wasserkochers als auch durch Verdunstung von Wasser an der Wasseroberfläche.
Insofern stimmt deine Beobachtung: je höher die Temperatur, desto langsamer die Erwärmung.
Gilt aber nur in erster Näherung.