Abwurfwinkel bei schrägem Wurf (Mechanik)?
Ich bräuchte Hilfe bei dieser Aufgabe. Am besten einen ausführlichen Rechenweg. Vielen Dank für die Hilfe im Voraus.
A: Ein Ball soll von 2 m über dem Boden über eine 10 m hohe und 2 m entfernte Mauer geschossen werden. Dabei kann der Abwurfwinkel Alpha gegen die Horizontale kontinuierlich von 0 (waagerecht) bis 90 (senkrecht) eingestelt werden. Die Abschussgeschwindigkeit ist fest auf den Betragd Vo = 20 m/s eingestellt.
Für welche Werte von Alpha kann der Ball über die Mauer geschossen werden?
Bist Du in der Oberstufe (welches BL)? Oder an der Uni?
An der Uni.
2 Antworten
hello… sorry, habe Mist gebaut… . Falsche Beziehung verwendet… ich schau mit das nun wieder an.
So, jetzt aber . . .
du nimmst die Bahngleichung von Spikeman, setzt die Zahlenwerte ein und drückst dann den cos^2 durch 1 / (1+tan^2) aus
das gibt eine quadratische Gleichung für den tan . . . kann man ohne Numerik lösen
die lautet bei mir
-159 = tan^2 - 40*tan
mit den Löungen Tan -1 = 35,5 und Tan-2=4,5 die entsprechenden Winkel sin 88,4 Grad und 77,5 Grad
Antwort auf Frage: Die beiden Winkel geben die Grenzwerte an; bei kleiner als 77,5 Grad fliegt der Ball an die Wand .. bei größer als 88,35 Grad trifft der Ball beim runterfallen ebenfalls die Wand. Bei den großen Winkeln ist die Funktionslösung sehr abhänig von den Rundungen. bei 88,35 Grad passt es , bei 88,4 Grad trifft der Ball vor der 10m Höhebeim runter Fallen die Wand: grüne Linie
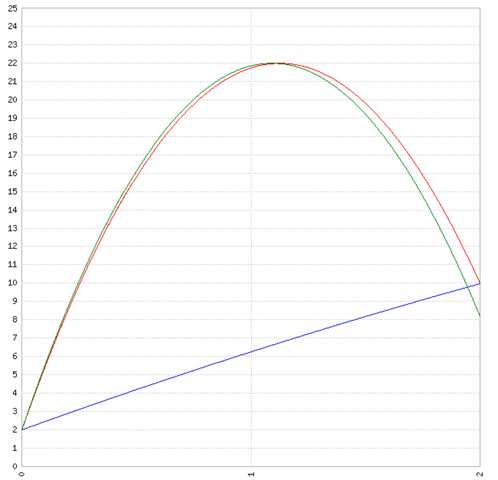
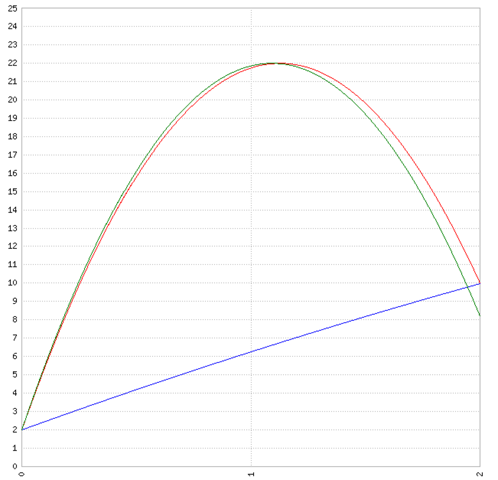
Sind nur diese beiden Winkel möglich oder auch alle dazwischen liegenden?
Ich schick dir ein paar Zeilen…. Schau aber nochmal drauf, habe etwas unübersichtlich geschrieben….. vlt habe ich mich vertan…. Vx ist die x Komponente von v0
Hüstel...musste ich noch nie machen...
Der Abschusswinkel muss größer als 76° sein, weil sich das aus dem Dreieck ergibt.
Ansonsten nimmt man halt die Formel für die x-y-Kurve, setzt x=2 m, ho=2 m, Vo=20 m/s UND y>10 m und löst nach dem Abschusswinkel auf!
Habe mich vertan, ist zwar eine quadratische Gleichung aber nicht im Argument sondern im Ausdruck des Tangens, also ohne Numerik lösbar. die beiden Grenzwerte des Abschußwinkels sind 77,5 und 88,4 Grad
Ja, genau… habe ich auch angesetzt, komme dann aber auf eine quadratische Gleichung für den Tangens und die ist nur numerisch lösbar…
Wie komme ich genau auf diese Formel und wie löse ich die denn nach Alpha auf?
Das ist die Bahnkurve des schrägen Wurfes…. Entweder herleiten oder nachgucken
Leider gibt es keine zusätzlichen Informationen. Wie würde man die Aufgabe denn mit der quadratischen Gleichung für den Tagens lösen?