Zweizeiliges Gleichungssystem lösen?
Guten Tag,
ich habe gerade Schwierigkeiten dabei ein zweiteiliges lineares Gleichungssystem zu lösen, da ich nicht genau weiß wie man das macht, da man ja normalerweise bei einem dreizeiligen LGS die 3 Variablen unten links, links in der Mitte und unten in der Mitte auf 0 umformt. Dies scheint bei einem zweizeiligen aber nicht so leicht möglich. Kann mir jemand erklären, wie man das macht? Im Bild sieht man die Werte des LGS, danke im Vorraus.
Mit freundlichen Grüßen,
Pikerg
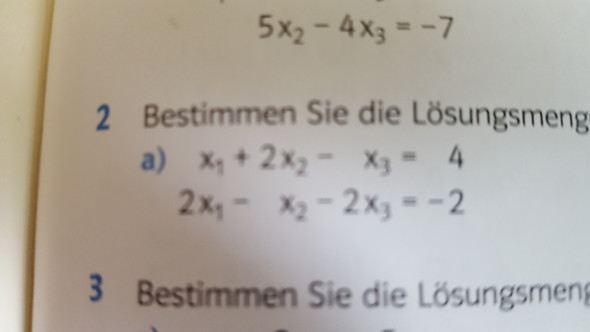
4 Antworten
I.) x_1 + 2 * x_2 - x_3 = 4
II.) 2 * x_1 - x_2 - 2 * x_3 = -2
Das sind 2 Gleichungen, aber 3 Unbekannte Variablen.
Deshalb handelt es sich um ein sogenanntes unterbestimmtes Gleichungssystem.
Es können deshalb (3 - 2) = 1 Variablen frei gewählt werden, die anderen beiden Variablen hängen deshalb von der frei gewählten Variablen ab.
Dabei spielt es meistens / oftmals keine Rolle, welche der Variablen man als frei Wählbar wählt, deshalb gibt es mehrere Möglichkeiten.
Es ist aber häufig üblich, die Variablen mit dem kleinsten Index als frei wählbar zu wählen. Man rechnet dann von "hinten nach vorne", stellt also zunächst nach der Variablen mit dem höchsten Index um, danach nach der mit dem zweithöchsten Index und so weiter.
Bei der freien Wählbarkeit kann es Einschränkungen geben, zum Beispiel, dass bestimmte Werte nicht erlaubt sind, weil es sonst zur Division mit Null kommt u.ä., dass muss man dann extra mit bei schreiben; kommt aber in deinem Beispiel nicht vor.
I.) x_1 + 2 * x_2 - x_3 = 4
II.) 2 * x_1 - x_2 - 2 * x_3 = -2
I.) nach x_3 auflösen :
I.) x_3 = x_1 + 2 * x_2 - 4
x_3 in II.) einsetzen :
II.) 2 * x_1 - x_2 - 2 * (x_1 + 2 * x_2 - 4) = -2
II.) nach x_2 auflösen :
II.) x_2 = 2
x_2 in die Gleichung für x_3 einsetzen :
I.) x_3 = x_1 + 2 * 2 - 4 = x_1
Fazit :
x_1 = frei wählbar
x_2 = 2
x_3 = x_1
Hallo,
wenn mich nicht alles täuscht, ist dieses Gleichungssystem unterbestimmt, da du mehr Variablen als Gleichungen hast.
In diesem Fall hast du unendlich viele Lösungen, die aber in einer gewissen Abhängigkeit zueinander stehen. Um diese Abhängigkeit zu veranschaulichen, legst du eine der Variablen fest, bspw. x1=2 und rechnest anhand dessen die restlichen Variablen aus. Bitte korrigiert mich, falls etwas fehlt!
Man tut das deshalb, weil man so erstmal allgemein die Abhängigkeit komprimiert zusammengefasst hat. Wenn dich jetzt jemand nach drei konkreten Werten fragt (zur Erinnerung: Es sind unendlich viele möglich), kannst du einfach t als eine Zahl festlegen und in diese in die anderen Ergebnisse in der Lösungsmenge einsetzen! Somit bekommst du ganz schnell eine richtige Kombination.
Du hast drei Unbekannte, aber nur zwei Gleichungen. Das heißt, dass das LGS unterdefiniert ist. Als Hilfe kannst du als dritte Zeile eine "Null-Zeile" hinzufügen. Das Ergebnis des LGS wird in Abhängigkeit einer Unbekannten sein.
Das geht auch nicht mit exakten Lösungen, da du dafür 3 Gleichungen brauchst.
Du kannst nur je eine in der Abhängigkeit von zwei anderen ausrechnen.
Die Begriffe x₁ etc. verweisen aber evtl. auf Vektoren. Und dort kann genau das gewünscht sein wegen der so gen. linearen Abhängigkeit.
Ach ja: Um jetzt hier allgemein die Lösungsmenge, wie es ja in deiner Aufgabe gefordert ist, anzugeben, wählt man für eine der Variablen einen Platzhalter, bspw. x3=t und das setzt du dann in die Zeilen ein. In der Lösungsmenge steht dann also sowas wie L={2-t, 4t, t}