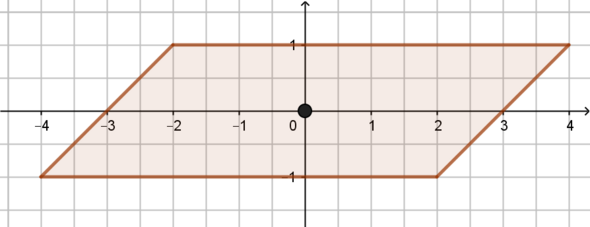
Wieso ist ein Parallelogramm punktsymmetrisch obwohl es keine Achsensymmetrie hat?
Im Internet steht z.b. auch dass das Drachenviereck keine Punktsymmetrie hat aber dafür eine Symmetrieachse und das alles checke ich nicht... Was heißt punktsymmetrisch überhaupt? Dass sich Diagonalen an einem Punkt kreuzen? Aber dann müsste ja im Prinzip auch ein Drachen punktsymmetrisch sein, was es aber nicht ist.
4 Antworten
Hallo,
Achsensymmetrisch heißt eine Figur (z. B. ein Viereck) genau dann, wenn du tatsächlich ein Spiegel auf die Symmetrieachse legen könntest und der Spiegel würde das verdeckte Stück perfekt ergänzen. Bei einem Drachenviereck geht das z. B.
Stell dir vor du suchst dir auf deinem Drachenviereck ein beliebigen Punkt mit dem Bleistift. Nun möchtest du diesen Punkt genau mit dem gespiegelten auf der anderen Seite verbinden. Das kannst du ein paar mal machen und wirst feststellen, dass diese Linien alle parallel verlaufen. Soweit so klar? Das behalten wir im Kopf.
Wie ist das nun mit der Punktsymmetrie? Nun ja, hier klappt der Gedanke mit dem Spiegel nicht. Aber irgendwie kann man trotzdem erkennen, dass jeder Punkt auf der Figur (z. B. dem Pralellogram) einen Punkt auf der anderen Seite hat. Versuchen wir jetzt dasselbe und verbinden einige dieser "Partner Punkte", stellt man fest, dass diese Linien nicht parallel sind - aber sich alle in einem Punkt schneiden!
Genau in diesem Fall kann man von einer Punktsymmetrie der Figur sprechen.
Achsensymmetrie ist der klassische Spiegel, entweder horizontal oder vertikal.
Punktsymmetrie bedeutet, dass eine Figur horizontal und vertikal gespiegelt ist.
Zeichne dir am besten kurz ein Koordinatensystem. In das zeichnest du jetzt die einzelnen Figuren (Parallelogramm, Drachen...) so, dass die Mitte genau auf dem Ursprung liegt. Und jetzt ziehst du eine Linie von einem der Eckpunkte deiner Figur zum Ursprung. Diese Line führst du jetzt so fort, dass sie gerade bleibt, also keinen Knick oder eine Kurve oder so etwas hat, und zwar genauso lange, bis die Linie doppelt so lang ist wie davor. So dass du jetzt praktisch zweimal die Linie vom Eckpunkt zum Ursprung hast, nur dass die eine direkt an der anderen dranhängt. Wenn dort, wo die lange Linie endet, ein weiterer Eckpunkt ist, dann kannst du dieses Verfahren mit allen anderen Eckpunkten wiederholen. Landest du von jedem Eckpunkt aus mit diesem Verfahren bei einem anderen Eckpunkt, dann ist deine Figur punktsymmetrisch.
Bei Achsensymmetrie verfährst du sehr ähnlich, nur dass du dieses Mal deine Linie nicht zum Ursprung, sondern zur y-Achse ziehst. Du legst deine Figur also wieder in ein Koordinatensystem, und zwar so, dass die Mitte der Figur auf der y-Achse liegt. Dann ziehst du eine Gerade, die parallel zur X-Achse verläuft, von einem Eckpunkt zur y-Achse und verdoppelst wiederum dann dort die Strecke. Auch hier gilt: Kommst von jedem Eckpunkt zu einem anderen, dann ist die Figur achsensymmetrisch (bezüglich der X-Achse).
Ich hoffe, ich konnte weiterhelfen, frag einfach, wenn du etwas nicht verstanden hast.
Stell dir hier das Parallelogramm vor:
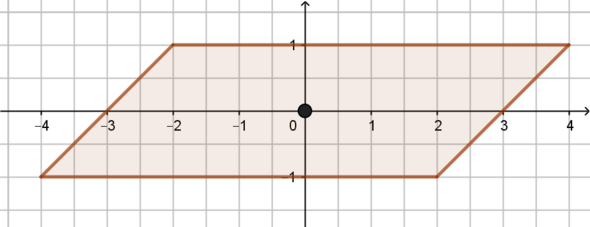
Drehst du jetzt das ganze Parallelogramm einfach um den schwarzen Mittelpunkt um 180°, hast du wieder genau deine Ausgangsfigur. Das bedeutet Punktsymmetrie.