Wie wandel ich die Normalform in die Scheitelpunkform um?
Moin Internetz, bin aktuell erkältet und muss jetzt Mathestoff nachholen, selbstständig und ohne Erklärung.. Jetzt hab ich hier sone Aufgabe wo ich dir Normalform in die Scheitelpunktform umwandeln muss, hab aber kein Plan wie das gehen soll.
Wäre sehr nett wenn mir jemand das erklären könnte.
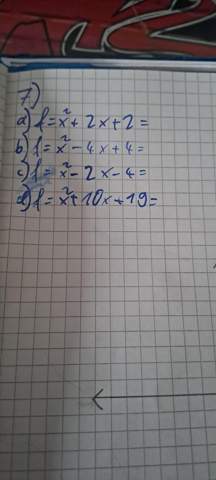
Das ist nur ein Bruchteil der Aufgaben (lasst euch nicht von dem f beirren kp was davor muss)
2 Antworten
Hallo.
Das geht mit der quadratischen Ergänzung.
https://studyflix.de/mathematik/quadratische-ergaenzung-1897
f(x) = x² + 2x + 2
= (x² + 2x + 1²) - 1² + 2
= (x+1)² - 1 + 2
= (x+1)² + 1
Dein Ergebnis kannst du auch kontrollieren, indem du einfach wieder die Klammern auflöst:
f(x) = (x+1)² + 1
= (x² + 2x + 1) + 1
= x² + 2x + 1 + 1
= x² + 2x + 2
Alternativ, indem du eine der Koordinaten vom Scheitelpunkt abliest und in die Normalform einsetzt:
f(x) = (x+1)² + 1 => SP(-1|1)
f(x) = x² + 2x + 2
f(-1) = (-1)² + 2*(-1) + 2
f(-1) = 1 - 2 + 2
f(-1) = 1
Passt also!
Viel Erfolg.
Allgemeine Form der Parabelgleichung ist: y = a x^2 + b x + c.
Es gilt:
a x^2 + b x + c = a (x^2 + b/a x + c/a) = a (x^2 + b/a + (b/(2a))^2) + c/a - (b/(2a))^2
= a (x+b/a))^2 + c/a - b^2/(4 a^2) = a (x+b/a)^2 + (4 a c - b^2)/(4 a^2);
dann einfach die Werte für a, b und c einsetzen…