Wie leitet man diese Funktion ab (mit euklidischer Norm)?

Hi,

weiß vielleicht jemand, wie ich

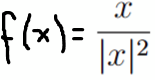
ableiten kann? IxI ist die euklidische Norm...

LG:)

Comments

[memon321]

Ist x hier ein Vektor aus R^n oder nur ein Skalar aus R?

[Qualle12]

Danke der Nachfrage, es handelt sich um einen Vektor aus R^n

Answer 1

[michiwien22]

Wenn x ein Vektor ist, was meinst du dann mit Ableitung eines Vektors?

Ist f(x) ein vektor?

$f\left(\vec{x}\right)=\frac{\vec{x}}{\left|\vec{x}\right|^2}$

Du schreibst nicht was du genau willst...daher das Schreiben einer Antwort Glaskugel-lesen.

Woher ich das weiß: Studium / Ausbildung – Studium technische Physik, promoviert in Festkörperphysik

Answer 2

[poseidon42]

Betrachte die Funktion:

f(x) = x/(|x|^2)

Man beachte die Identität: |x|^2 = x^2 für x aus IR.

--> f(x) = 1/x --> df/dx = (-1)/x²

Woher ich das weiß: Studium / Ausbildung – Studium der Elektrotechnik (Energie, Automatisierung)

Answer 3

[Roderic]

Falls x Element von R, dann ist |x|² dasselbe wie x².

Somit bleibt für f(x) übrig:

$f\left(x\right)=\frac{1}{x}$

Answer 4

[ScienceDaGuy]

Die Seite macht das für dich

https://www.wolframalpha.com/widgets/gallery/view.jsp?id=ecfd3a449d1c38d762d0ae078b7c7208&reportprob=1

Comments

[Halbrecht]

wenn man pro hat ?

[ScienceDaGuy]

@Halbrecht

Ne, tatsächlich auch so. Aber es gibt viele Programme online dafür so z. B. auch https://www.ableitungsrechner.net/

Answer 5

[memon321]

Die Quotientenregel kannst du hoffentlich selbst anwenden.

Comments

[Qualle12]

vielen lieben Dank:)