Wie könnt man das ausrechnen?
Guten Abend,
ich habe versucht diese Aufgabe zu lösen, konnte aber keine gescheite Lösung finden.
Die Aufgabe lautet: Miriam ( Augenhöhe 1,70m) steht auf dem 11m hohen Pier und schaut über das Meer zum Horizont. Der Erdradius beträgt 6371km. Berechne, wie weit sie sehen kann?
Ich habe es Skizziert und paar Wege probiert aber konnte nicht im Buch angegebene Lösung: 12,7 km nicht kommen.
Könntet ihr mir ein bisschen helfen.
Vielen Dank schonmal.
4 Antworten
Hallo marsel111,
Aus welchem Buch hast Du denn diese Weisheit? Die angegebenen 12,7km stimmen in der Praxis nämlich nicht wirklich.
Bei klarer Sicht würde Miriam tatsächlich bis zu 13,9km weit sehen.
Das Ergebnis im Buch bezieht sich auf die sog. geometrische Sichtweite - und die kannst Du über den Pythagoras berechnen, indem Du Dir ein rw. Dreieck vorstellst mit den 3 Seiten:
s: Sichtweite
R: Erdradius
c: Erdradius + Höhe des Aussichtspunktes (Hypothenuse) = R + h
Als Formel ergibt sich dann: s² + R² = (R + h)², alle Werte in km einsetzen!
In der Praxis wird die Sichtweite jedoch noch durch die Atmosphärische Refraktion, d.h. Lichtbrechung durch die unteren Luftschichten beeinflusst, die hier, sehr vereinfacht gesagt, praktisch wie eine Linse wirken und die Lichtstrahlen etwas krümmen, sodass man noch eine Kleinigkeit "hinter den Horizont" sehen kann.
Die Sichtweite unter Berücksichtigung der Lichtkrümmung verhält sich dabei so, als wäre die Erdkugel scheinbar grösser, also so, als hätte sie einen grösseren Radius.
Für die näherungsweise Berechnung inclusive Krümmung kann man dann genau dieselbe Formel von oben verwenden, man muss nur den wahren Erdradius (auch der ist ja gemittelt, da die Erde in Wahrheit keine strenge Kugel ist) durch den gemittelten, scheinbaren Erdradius bei Lichtrefraktion ersetzen. Und dieser beträgt anstatt 6371km dann 7680km. Und wenn Du den in die pythagoräische Formel einsetzt und nach s auflöst, dann kommst Du eben auf die realen 13,9km anstatt der geometrischen 12,7km.
2 x 6371 x 0,0127 und daraus die Wurzel ziehen
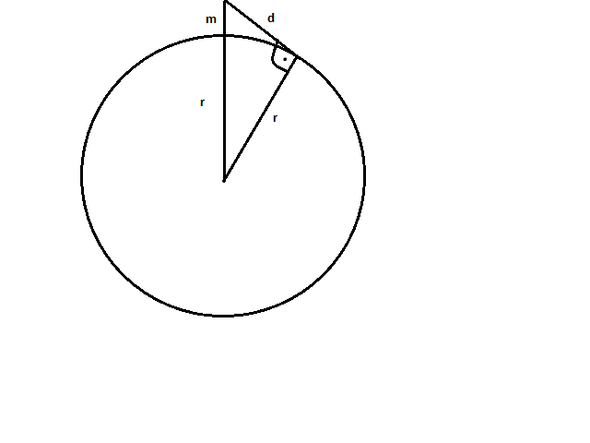
Ich hab unten mal ne Skizze eingefügt... m ist der Abstand von der Erde zu Miriams Augen (wie groß ist m also?), r ist der Erdradius und d ist die gesuchte Sichtweite. Da die maximale Sichtweite tangential zur Erde zeigt, ist das eingezeichnete Dreieck rechtwinklig. Mit dem Pythagoras gilt:
(m + r)² = r² + d²
=> d = Wurzel ((m + r)² - r²).
Die Frage ist nicht eindeutig gestellt. Es fehlt die Angabe, wohin Miriam sehen soll. Wenn sie in Richtung Horizont blickt, kann sie knapp darüber Millionen km weit sehen.
Natürlich kann man ahnen, welche Rechnung angestellt werden sollte.
Rechne mit dem Satz des Pythagoras das -vom Lehrer erwartete- Ergebnis aus. Und sage ihm, dass die Aufgabe falsch gestellt wurde.
In der Aufgabe steht aber nicht, dass Miriam in Richtung Horizont blickt, sondern zum Horizont. Das ist schon eine Nummer eindeutiger.