Wie geht diese Matheaufgabe (mit Wurzeln Linie in Rechteck berechnen)?
Wir schreiben sehr bald eine Mathe-Klassenarbeit und ich kann meine Mathelehrerin vorher nicht fragen. Jetzt müssen wir es für die Arbeit können und meine Freunde verstehen es auch nicht.
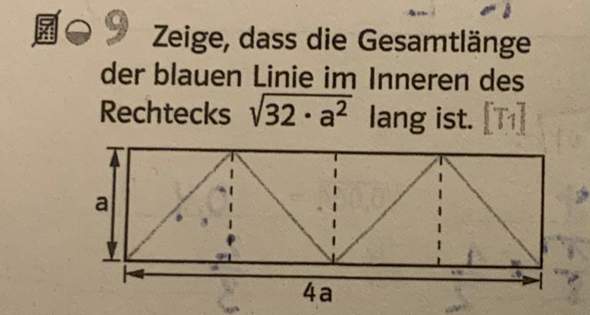
Ich habe das Rechteck zerlegt und zu einem Quadrat zusammengesetzt. Hierbei war der Flächeninhalt 2a•2a=4a^2. Stimmt das überhaupt und wie soll ich nun weitermachen?
Danke im Voraus!
3 Antworten
ANderER WeG :
.
vier Quadrate nebeneinander mit Seitenlänge a
.
Man braucht die Diagonale d .
Dafür Pythagoras
w heißt wurzel
d² = a² + a²
d = a*w(2)
.
4 * a*w(2) =
2² * a * 2^(0.5) =
2^(2+0.5) * a =
2^(2.5) * a
.
32 = 2^5
w(32) = 2^2.5
w(a²) = a
.
also auch 2^(2.5) * a
Ein Viertel der gesamten blauen Linie ist gleich der Diagonalen des Quadrates mit der Seitenlänge a
Die Länge der Diagonale ist a∙√2
Die blaue Linie ist also 4∙(a∙√2) = √16∙(a∙√2) = a∙√32 = √(a²∙32)
Wenn die 4 Diagonalen gemeint sind :
Gib a den Wert 1, dann hat jedes Quadrat eine Diagonale von √2. Das Mal 4 = ca 5,6....5,7......5,656854249492 genau. Das multiplizieren und du bekommst 32.
Jetzt fügst du 1 in die Formel mit der 32 Mal a²,. Du erhälst √32 als Ergebnis.