Wie funktioniert das auflösen der Binomischen Formel Hoch 3 (Siehe Anhang)?
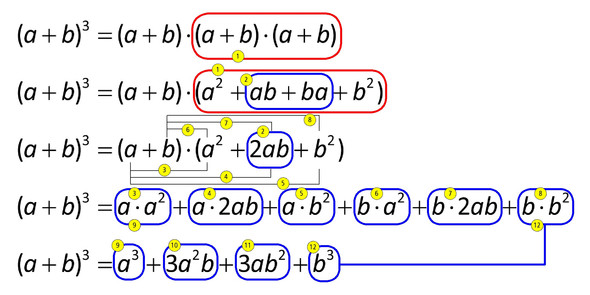
Ich habe ein Bild als Anhang ergänzt. Die Formelauflösung ist mit Positionsnummern dargestellt. Bei Position 10 und 11 bin ich hängen geblieben. Für die Auflösung wäre ich sehr dankbar.
Mit besten Grüßen Mark
5 Antworten
Das ist simpel. Wegen der Kommutativität (Vertauschbarkeit) der Multiplikation ist
a * 2ab = 2 a² b und auch
b a² = a² b
Wenn du die beiden addierst, hast du 3 a² b
Genauso beim anderen Term.
Meine Empfehlung ist immer, die Terme sofort bei Auftreten in
lexikographischer Reihenfolge zu schreiben (also gemäß dem Alphabet wie in einem Lexikon). Dann musst du in einer längeren Aufstellung, in der sonst z.B. abc, bca, cab, ... vorkämen, nicht lange nach denen suchen, die man aufaddieren kann.
a²b und ab² sind allerdings etwas Verschiedenes - wie hier ja auch.
Naja einfach
a^2+2ab+b^2 *(a+b)
= a^3 + 2a^2*b + ab^2 + a^2*b + 2ab^2 + b^3
Das kannst du zsmfassen (2a^2*b + a^2*b = 3a^2*b, gilt für 3ab^2 ebenso
Bei 10 und 11 wurde auf folgenden Schritt nicht näher eingegangen:
a*2ab=2a^2*b
b*2ab=2a*b^2
Danach wurden halt die Buchstaben nach Potenzen sortiert und zusammengefasst.
10=4+6
11=5+7
Dafür zieht man bei der 4 das a und bei der 5 das b rein, sodass dort 2ba^2 bzw. 2ab^2 steht und dann kann man es mit 5 bzw 7 addieren ;-)
In der vorletzten Zeile hast du einmal den Summanden
a * 2ab (das ist die 4)
und einmal den Summanden
b * a² (das ist die 6).
Wenn du das ausmultiplizierst und umsortierst, dann hast du
2 a²b
und
a²b.
Das kannst du dann zu (10) zusammenfassen und erhälst
3 a²b.
Genauso ist das mit
a * b² (5)
und
b * 2ab (7)
Das ist nichts anders als
ab²
und
2ab²
- macht zusammen 3ab², und das ist (11).