Wie erkennt man punktsymetrische Figuren?
Siehe Bild.
Ich will gar keine Lösung, sondern nur wissen wie man es erkennt.
Sind es alle außer die letzte?
5 Antworten
Stell dir vor, du schneidest eine Figur in der Mitte auseinander. Dann spiegelst du den oberen Teil davon einmal nach unten und einmal entweder nach links oder nach rechts. Wenn dieser Teil dann genauso aussieht, wie der zweite, untere Teil, dann ist etwas punktsymmetrisch.
Hier sind alle Figuren punktsymmetrisch, soweit ich weiß.
Eine Punktspiegelung ist das selbe, wie eine Drehung um 180°. Wenn es also möglich ist eine Figur um 180° zu drehen und sie hinterher genau so aussieht, ist sie Punktsymmetrisch.
Ich kannte den Begriff gar nicht und musste erst einmal googeln. Schau mal bitte hier.
https://de.serlo.org/mathe/geometrie/grundbegriffe/symmetrie/punktsymmetrie
Wenn ich das so sehe, sind all die Figuren punktsymetrisch. Und wenn ich die halbe Textzeile richtig deute, sollst Du den Spiegelpunkt einzeichnen.
Gruß Matti
Natürlich. Sonst würde die Figur nach einer Drehung um 180° ja nicht genauso aussehen wie vor der Drehung.
Herzliche Grüße,
Willy
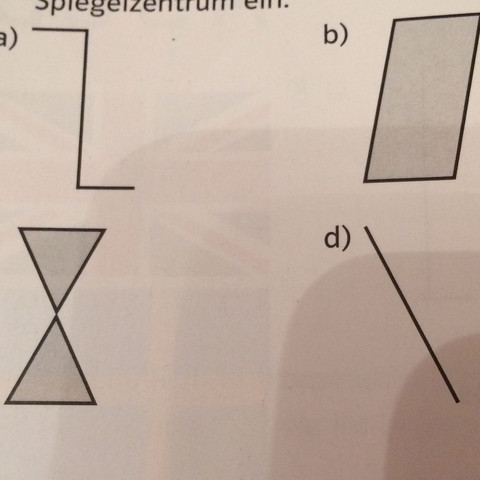
Beim Parallelogram (Deine Figur unter b) ist das mit der Mitte so eine Sache, aber im Prinzip hast Du recht. Wie in dem Link zu sehen, verbindest Du die gegenüberliegenden Ecken mit einer gedachten Linie und wo sich die beiden Linien kreuzen ist die Mitte. Bei der Figur c) ist es genau der Punkt, wo sich die beiden Spitzen der Dreiecke treffen. Bei der Linie und bei der Figur a) ist es genau die Mitte der Linie.
Mach nächstes Mal ein Bild von der gesamten Aufgabe, damit man vollständige Informationen hat.
Bei achsensymmetrischen Figuren verbindest du die Original- und Bildpunkte mit gleich langen Senkrechten, die auf der Spiegelachse stehen.
Bei punktsymmetrischen Figuren verbindest du Original- und Bildpunkte durch Strecken, deren Mitte der Spiegelpunkt ist.
(Eine Gerade oder Strecke ist per se punktsymmetrisch, ein Strahl nicht.)
Das sind alle. Und du sollst den Spiegelpunkt setzen.
Danke und der liegt genau in der Mitte, oder ?