Wie beweise ich das der Rand einer Menge abgeschlossen ist?

- Hallo. Ich bezeichne
dM:= {Randpunkte von M} den Rand. und
d^M^:= dM vereinigt {HP von dM}. Abschluss.
im Prinzip muss ich ja zeigen das
dM = d^M^ . Die einer Richtung ist ja klar. Aber wie beweise ich die andere? Komme überhaupt nicht weiter hab das durch wiederspruch und auch direkt versucht. Danke
4 Antworten
Zeige die folgende Gleichheit, dann folgt die Behauptung direkt, weil beide Mengen rechts abgeschlossen sind.
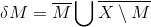
Vorsicht, ich hab ein Delta aus Versehen verwendet.^^
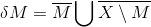
Vergiss beide Kommentare. Ich weiß nicht was los ist, aber es gehört ein geschnitten und kein vereinigt hin.
Achso das habt ihr auch noch nicht bewiesen. Wenn du willst kann ich dir den Beweis kommentieren. Aber als Antwort hier drunter geht es leider nicht, da ich LaTeX brauche (sonst wird es unleserlich). Oder weißt du auch nicht was M mit dem Strich bedeutet?
Ich weiß die Bedeutung von M mit strich. Wo kannst du mir dann den Beweis zeigen?
Ich schreib unter dieser Frage (nochmal) eine Antwort. Nur hier (also unter einer anderen Antwort) ist es nicht möglich ein Bild einzufügen.
Meist stehen Aufgabenteile ja nicht ohne Hintergedanken nacheinander da. Aus a) erhält man doch, dass der Rand von M das Komplement des Inneren von M im Abschluss von M ist (denn der Abschluss ist nach a) ja disjunkte Vereinigung von Innerem und Rand!).
Das Innere von M ist eine offene, der Abschluss von M eine abgeschlossene Teilmenge von X. Ich glaube, damit ist man dicht vorm Ziel.
”Aus a) erhält man doch, dass der Rand von M das Komplement des Inneren von M im Abschluss von M ist”
was ist das in Zeichen ausgedrückt? Ich versteh das nicht wörtlich
Rand(M) = Abschluss(M) \ Inneres(M)
= (X \ Inneres(M)) geschn. mit Abschluss(M).
also Durchschnitt zweier abgeschlossener Mengen, also abgeschlossen.
(In die erste Zeile gehört kein Zeilenwechsel, aber GF setzt einen.)
Wobei:
Das c im Exponenten soll Komplement bedeuten
Dann mit den Eigenschaften eines top. Raumes argumentieren. Komplement einer offenen Menge ist abgeschlossen. Vereinigung offener Mengen ist offen, usw. wenn ihr das noch nicht hattet, RIP.
In deinem Beweis benutzt du dass dsr Rand abgeschlossen ist (also das was zu zeigen ist) Nur damit kannst du zeigen dass die erste Menge offen ist.
Schreib mal zurück, was der Korrektor sagt, wenn du das echt abgibst.
Ich krieg es irgendwie nicht hin die Bilder anzuheften. :D ich probiers nochmal
Sorry ich muss sagen ich bin zu unfähig hier die Bilder richtig reinzukriegen.
Kannst du vielleicht mir die Bilder privat schicken?
Ich habe meine email Adresse als Freundschaftsanfrage geschickt
Warum sind beide Mengen rechts abgeschlossen?