Wie bestimmt man bedingte Wahrscheinlichkeiten, wenn die Bedingung eine Schnittmenge ist?
In der Aufgabe geht es um ein Tetraeder, wovon drei Seiten einfarbig blau, gelb und rot sind. Die vierte Seite hat alle drei Farben. Es sollen jetzt die Ereignisse untersucht werden, dass jeweils eine Seite "gewürfelt" wird - A: blau; B: gelb; C: rot. Speziell gefragt ist nach W(A|(B∩C)). Die Wahrscheinlichkeiten der Ereignisse A, B und C sind jeweils 0,5, da jeweils 2 von 4 Seiten die gleiche Farbe tragen.
Das Ergebnis ist 1, was im Sachzusammenhang klar ist, denn unter der Bedingung, dass gelb und rot auftreten - da trifft nur die bunte Seite 4 zu - ist das Ereignis A, also blau tritt auf, sicher. Allerdings ist zu dem Ergebnis keine Rechnung gegeben, falls man das überhaupt berechnen und nicht nur im Zusammenhang erklären kann.
In meinen Rechnungsversuchen kann ich die Wahrscheinlichkeiten immer so kürzen, dass ich bei 0,5 lande. Meine Vermutung: Ich mache einen Fehler bezüglich Unabhängigkeit, aber bisher erschließt es sich mir nicht.
Ich suche also nach einer allgemeinen Formel, wie man eine bedingte Wahrscheinlichkeit berechnet, wenn die Bedingung eine Schnittmenge beinhaltet, oder nach einer Erklärung, was ich falsch mache.
Schon einmal danke im voraus!
1 Antwort
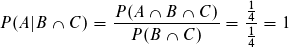
Macht auch Sinn, da die Schnittmenge von A und B das Ereignis der Seite mit allen Farben ist. Da wir nur diese eine Möglichkeit betrachten (ist ja eine bedingte Wahrscheinlichkeit) ist Wahrscheinlichkeit entweder 0 oder 1. Da zu A aber auch die Seite mit allen Farben gehört, ist die Schnittmenge von A und B und C ebenfalls die Seite mit allen Farben. Somit ist Wahrscheinlickeit 1.
Ich hoffe, es ist einigermaßen verständlich und dass ich helfen konnte :)
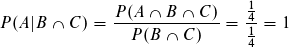
Ja, das hat mir tatsächlich sehr geholfen! Ich bin - warum auch immer - nicht auf die Idee gekommen, den Zähler so zu formulieren; stattdessen hab ich versucht Produkte zu bilden, wo ich dann aber immer die Bedingung kürzen konnte ^^
Danke Dir und einen schönen Abend!