wie berechnet man die wurfweite(z.B. eines speers)?
Aufgabenstellung:
Die flugbahn eines speer ist nahezu parabelförmig. Der Abwurfpunkt A liegt 1,80 über der Abwurflinie. Der Speer erreicht nach 20 m, in horizontaler Richtung von der Abwurflinie, seine Maximale Höhe von 9,80 m.
Könnt ihr mir dabei helfen, es ist dringend
Ein bild kann ich leider nicht schicken
Danke
2 Antworten
Neben dem (schöneren) Ansatz über die Scheitelpunktsform könntest du die drei Koeffizienten a,b,c in f(x) = a x² + b x + c aus den folgenden drei Angaben bestimmen:
- Abwurfpunkt: f(0) = 1,8 --> c = 1,8
- Hochpunkt: f(20) = 9,8 --> a * 20² + b * 20 + 1,8 = 9,8
- Hochpunkt: f'(20) = 0 --> 2 * a * 20 + b = 0
- I: 400 a + 20 b = 8
- II: 40 a + b = 0 --> 400 a + 10 b = 0
I-II: 10 b = 8 in II: 400 a = -8
- b = 8/10 = 0,8
- a = -8/400 = - 1/50 = -0,02
f(x) = -0,02 x² + 0,8 x + 1,8
Die rechte (positive) Nullstelle ist der Punkt, an dem der Speer landet, also die Wurfweite.
Na wenn der Scheitelpunkt mit S(20/9,8) gegeben ist, bietet sich als Ansatz doch die Scheitelpunktform an:
f(x) = a(x - d)^2 + e
mit S(d/e)
Daher:
f(x) = a(x - 20)^2 + 9,8
Fehlt noch a und das kriegen wir mit dem Abwurfpunkt A hin:
A(0/1,8)
Das setzen wir ein:
1,8 = a(0 - 20)^2 + 9,8
a(- 20) ^2= -8
a = 8/400 = -0,02
Damit:
f(x) = -0,02(x - 20)^2 + 9,8
wenn man die Klammer ausmultiplizert erhält man die Normalform.
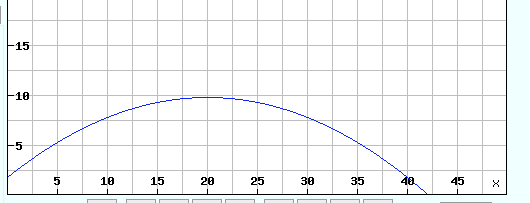
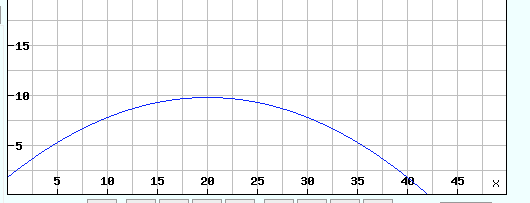
Und so sieht das als Graph aus: