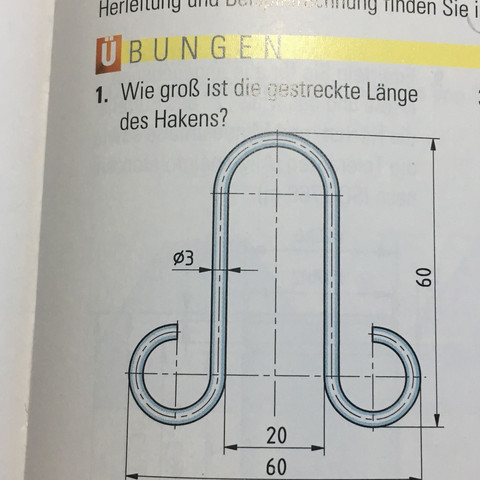
Wie berechnet man bei der Aufgabe die Gestreckte Länge?
Ich schreibe morgen eine Arbeit darüber und kann das nicht
7 Antworten
Hallo iamkmmmi,
zuerst Rechnest du den Umfang eines der hypothetischen Kreise (unten links oder rechts) aus. Der Durchmesser beträgt wie man ablesen kann 20mm. Das Ergebnis nimmst du mit 0,75 mal um das offene viertel wegzunehmen.
Dann rechnest du die gerade Linie +. Das sind 40mm. Nun haben wir an der Spitze wieder ein Viertel eines Kreises den wir berechnen müssen. Der Radius beträgt hier 10mm. Nachdem wir wieder einen vollen Kreis berechnet haben, nehmen wir das Ergebnis diesmal mit 0,25 mal, damit wir nur das eine Viertel haben.
Dann können wir alles zusammenrechnen und danach mit 2 mal nehmen da wir nur eine Hälfte berechnet haben.
Wenn man nun die ausgerechnete Länge nimmt und mit 3mm mal nimmt bekommen wir ebenfalls den Flächeninhalt raus.
Falls ich keine Denkfehler habe, sollte dies die richtige Lösung sein. Du musst nur noch rechnen. :D
Liebe Grüße,
Hydro
Gesucht ist also die Länge der gestrichelten Linie.
Wir beginnen unten links.
Dort hast eine Dreiviertelöse mit 20 mm Außendurchmesser und damit 10 mm Radius außen. Um auf die gestrichelte Linie zu kommen, musst noch eine halbe Drahtstärke abziehen, 1,5 mm. Das ergibt den mittleren Radius von 8,5 mm.
Der mittlere Umfang einer Vollöse wäre
U = 2 π r = 2 π 8,5 mm = 53,41 mm
Da zwei Dreiviertelösen hast, links und rechts, brauchst 2 • 3/4 = 6/4 = 3/2 = 1,5 Vollösen
(1) 3/2 • 53,41 mm = 80,11 mm
Der obere Halbbogen des Hakens hat 20 mm Innendurchmesser und damit 10 mm Innenradius. Der Außenradius beträgt 13 mm, nämlich die gesamte Drahtstärke mehr.
Der mittlere Radius beträgt Innenradius zuzüglich eine halbe Drahtstärke, also insgesamt 11,5 mm.
Der mittlere Umfang des Halbbogens ist
(2) U / 2 = π r = π 11,5 mm = 36,13 mm
Um die Länge eines geraden Stücke zu bekommen, ziehst von der Gesamtlänge 60 mm unten und oben jeweils einen Außenradius ab, also
L = 60 mm - 10 mm - 13 mm = 37 mm
Wir haben davon zwei, links und rechts. Das ergibt
(3) 2 • 37 mm = 74 mm
Das bauen wir jetzt zusammen:
Die gestreckte Länge des Hakens ist
S = (1) + (2) + (3)
= 80,11 mm + 36,13 mm + 74 mm
= 190,24 mm
Ist das soweit verständlich für Dich?
Gut.
In der Zeichnung übersiehst leicht, dass die Maße nicht an der Mittellinie anliegen, sondern mal innen, mal außen. Auf solche Feinheiten musst unbedingt achten beim Lösen solcher Aufgaben.
Also ich habe bei den beiden 270° Bögen jeweils gerundete 40,1mm, bei den geraden Teilen jeweils 40mm, und beim 180° Bogen habe ich gerundete 36,1mm.......
bei den unteren Bögen kannst den mittleren Umfang berechnen 1-25 - ebenso bei dem oberen Halbbogen - die Geraden kannst auch ausrechnen - alle Maße vorhanden
Erst 2 mal den 3/4 Umfang der äußeren Kreise berechnen, dann 2 mal die die geraden Strecken ohne Krümmung und dann noch den halben Umfang des oberen Kreises und am ende alles zusammenzählen
(was haben sich die "bildungsexperten " sich eigentlich bei dieser form gedacht?^^)
Woher weis man welchen Durchmesser die Kreise links und rechts haben ? Und ja das stimmt xD
Das ist leider nicht ganz richtig.
Die beiden Dreiviertelösen haben 20 mm Außendurchmesser, der obere Halbbogen 20 mm Innendurchmesser.
Unten ergibt sich damit ein Radius von 8,5 mm, 10 mm abzüglich halber Drahtstärke, oben von 11,5 mm, 10 mm zuzüglich halber Drahtstärke.