Wie berechne ich einen Kegelstumpf, wenn nur der Grundkreisradius und die Höhe angegeben sind?
Hallo!
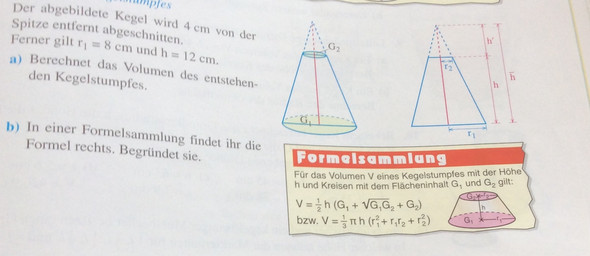
Ich möchte gerne wissen, wie ich das Volumen eines Kegelstumpfes berechne, wenn nur die Höhe und der Grundkreisradius angegebn sind.
Der Kegel ist ursprünglich 16 cm hoch, wurde aber 4cm unter der Spitze abgetrennt, dazu ist noch der Grundkreisradius von 8cm angegeben. Allerdings ist die mir einzig bekannte Formel zum Berechnen des Volumen eines Kegels so, dass ich den Flächeninhalt der 2 (kleineren) Grundkreisflächd wissen muss. Diese kann ich aber nicht berechnen, weil ich nur eine Angabe kenne, nämlich die 4cm Höhe des kleinen Kegels.
Die Höhe der Seitenfläche des kleinen Kegels lässt sich nicht berechnen, da ich um die Seitenfläche des Kegelstumpfes berechnen zu können und später die Gesamthöhe der Seitenfläche abziehen zu müssen, damit ich die Differenz kenne wissen muss welche Maße der Radius der zweiten Grundfläche hat. Diese müsste ich dann vom Grundkreisradius abziehen, damit ich mithilfe des Satz des Pythagoras die Seitenfläche berechnen kann.
Fakt ist, dass ich zum Berechnen der Seitenfläche des Kegelstumpfes nur die Höhe kenne (12cm).
Wie zur Hölle soll ich dann bitte das Volumen des Kegelstumpfes berechnen?!
Bitte helft mir, denn unser Mathelehrer hat uns keine Formel zur Berechnung genannt.
Wie lautet die Formel die ich anwenden muss?
3 Antworten
Hallo,
Du kannst den Radius der Plattform mit Hilfe des Strahlensatzes berechnen.
Es gilt: 8/16=x/4, also x=2, der Radius des kleinen Kreises.
Nun brauchst Du nur noch vom Volumen eines Kegels mit 16 cm Höhe und 8 cm Radius das Volumen der abgesägten Kegelspitze mit 4 cm Höhe und 2 cm Radius abzuziehen.
Herzliche Grüße,
Willy
Was? Du kennst die Strahlensätze nicht? So kannst Du in Mathe nicht überleben.
Sieh mal schnell hier nach:
https://www.youtube.com/watch?v=cACn06wXkYY
Alles Gute,
Willy
Was soll ich sagen...Gymnasium und G8 halt
In der oberen Formel auf dem Blatt ist übrigens ein Fehler:
V=(1/3)h* usw., nicht (1/2)h
Willy
Aufgrund des Strahlensatzes gilt
h' / h = r2 / r1
4 / 12 = r2 / 8
8/3 = r2
und das in
V = 1/3 * pi * h (r1^2 + r1r2 + r2^2)
einsetzen.
Du hast den Strahlensatz falsch angewandt:
Es muß heißen:
(h'+h)/h'=r1/r2, also 16/4=8/r2
Dann ist r2=8*4/16=2
Herzliche Grüße,
Willy
Du kennst nicht nur die Höhe des Stumpfes, sondern auch die Höhe des abgesägten Stücks.
Die Formel für einen Kegel, der bis zur Spitze geht, solltest du auch kennen. (Tipp: sonst nimm die Formel für einen Kegelstumpf für den Fall, dass der kleinere Radius 0 ist.)
Dann die entscheidende Idee: Restvolumen = Gesamtvolumen - abgesägtes Volumen
In einem Eimer sind 5 l Wasser. Du gießt 2 l raus. Wie viel ist noch drin?
Ein Balken hat ein Volumen von 50 l. Du sägst ein Stück von 15 l Volumen ab. Welches Volumen hat das Reststück?
Ein Balken hat einen Querschnitt von 10 cm * 10 cm und eine Länge von 5 m. Du sägst ein Stück von 1,50 m Länge ab. Welches Volumen hat das Reststück?
Ein Kegel hat einen Grundkreisradius von 8 cm und eine Höhe von 16 cm. Du sägst von der Spitze aus einen 4 cm langen Kegel ab. Welches Volumen hat das Reststück?
Vielen Dank für deine Antwort!
Ich war schon am verzweifeln, weil unser Mathelehrer uns nichts dazu erklärt hat und es im Anschluss dann auch noch als Hausaufgabe aufgab.
Von dem Strahlensatz habe ich im Übrigen noch nie etwas gehört. hoffentlich wird er es nächste Stunde noch einmal erklären :)