quadratische Pyramide?

Die Aufgabenstellung lautet:

Ermitteln Sie, wie groß der Winkel zwischen zwei diagonal gegenüberliegenden Seitenkanten an der Spitze der Pyramide ist.

Neigungswinkel der Seitenfläche zur Basisfläche, Alpha = 51,85°

die Basiskanten a betragen 230,3 m,

die Höhe beträgt 146,59 m und

Ha = 186,41.

s habe ich mir ausgerechnet. s = 219,13

Wenn ich dann eine Skizze mache und den Winkel an der Spitze rechne kommt jedoch wieder ein falsches Ergebnis. 

Es sollen 96° sein. Wie komme ich auf das richtige Ergebnis?

Meine Skizze wäre das:

Answer 1

[Wechselfreund]

Skizze machen.

Betrachte das Dreieck aus Flächendiagonale der Grundfläche und zwei Seitenkanten. Symmetrieachse Höhe ermöglicht den Tangens des halben Winkels.

Comments

[Fyuwjsjsn]

Ich habe meine Skizze angehängt. Könntest du mir sagen wo die Fehler sind?

Answer 2

[merkurus]

Berechnung
Geg.: a = 230,3 m ; α = 51,85 ; h = 146,59 m
---
d/2 = Wurzel( (a/2)² + (a/2)² )
d/2 = Wurzel( (230,3 / 2)^2 + (230,3 / 2)^2 )
d/2 = 162,8466917073 m
---
β = arctan( (d/2) / h ) * 2
β = arctan( 162,846692 / 146,59 ) * 2
β = 96,014 rd. 96°

Answer 3

[Halbrecht]

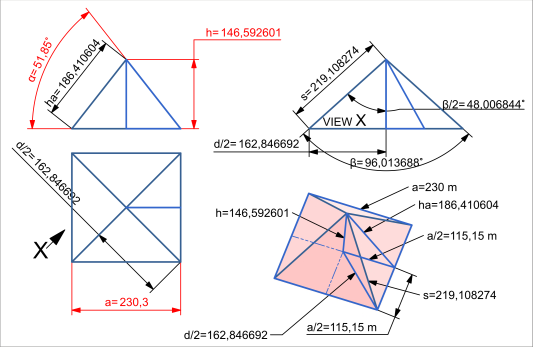
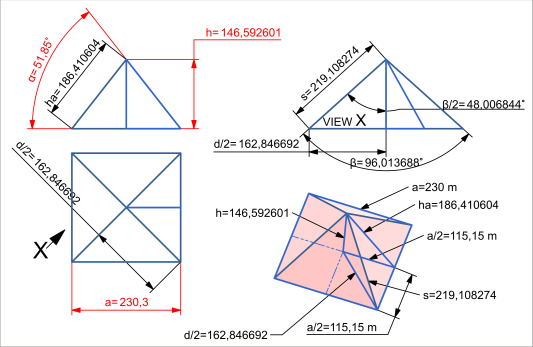
Das Dreieck besteht aus zwei gleichlangen Schenkeln s und der Grundseite Diagonale der Grundfläche

.

von diesem Dreieck die eine Hälfte

Grundseite halbe Diagonale

230.3/2 * wurz(2) 

eigentlich braucht man die Diagonale gar nicht , man kann gleich

cos(winkel) = Höhe/s = 146.59/219.13 rechnen

und kommt auf 48.01 Grad