Wie berechne ich das Volumen von dieser schrägen Pyramide?
Ich verzweifle ..
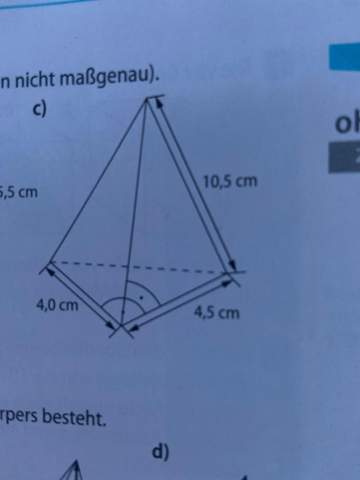
3 Antworten
Volumen Pyramide: V = 1/3 G*h
Grundfläche G ist ein rechtwinkliges Dreieck mit den Kathetenlängen 4,5cm und 4,0cm, also G = 1/2 * 4,5cm * 4,0cm = 9,0 cm^2
Wenn ich die Zeichnung richtig interpretiere, steht die vordere Kante der Pyramide senkrecht auf der Grundfläche, ist somit die Höhe h der Pyramide. Die hintere rechte Kante der Pyramide mit Länge 10,5cm ist somit die Hypothenuse der rechten dreieckigen Seitenfläche mit Katheten h und 2. Kathete mit 4,5cm Seitenlänge.
Nach Pythagoras gilt: h^2 + (4,5cm)^2 = (10,5cm)^2, also
h = Sqrt((10,5cm)^2-(4,5cm)^2) = Sqrt(110,25-20,25)cm = Sqrt(90)cm = 3*Sqrt(10)cm
Damit also:
V = 1/3 G*h = 1/3 * 9 cm^2 * 3*Sqrt(10) cm = 9*Sqrt(10) cm^3
Fertig!
Vielen Dank für die detaillierte Antwort. Ich bin auf 31,5cm^3 gekommen (Formel) V=
a * b * h / 6
mein h sind die 10,5 das stimmt dann wohl nicht. Allerdings kann ich ihr h nicht erkennen..
Die Pyramide ist wirklich Windschief.
Wenn die angegebenen Winkel bei der Grundfläche und der Höhe rechte Winkel sind (weil mit Punkt), ist es relativ einfach zu berechnen.
Zuerst mit Pytagoras die Höhe. (Die Höhe geht senkrecht hoch.)
h² + 4,5² = 10,5²
Danach nimmst du 3 identische Dreieckspyramiden dazu und erhälst eine normale Ägyptenpyramide.
Die berechnrst du normal und teilst das Ergebnis zusätzlich durch 4, weil du die 4fache Dreieckspyramide berechnet hast.
Grundfläche ist 4 x (4,0 x 4,5)/2
Also 2 x 4,0 x 4,5
für mich steht das Dreieck mit 10.5 und 4.5 senkrecht. Damit ist dessen Höhe die Höhe der Py .....
Wenn 10,5cm die Höhe wäre, müsste der rechte Winkel in der hinteren Ecke sein - die Zeichnung ist aber wirklich nicht besonders übersichtlich…
Das ist nur zur besseren vorstellung. In der Aufgabe wird eine geviertelte Pyramide berechnet.
Höhe bei mir 9,487 cm. Mal 4,5 x 4,0 ÷ 2 = 85,38 mal 1/3 = 28,46 cm³
Ja auf dieses Ergebnis bin ich dank eurer Hilfe auch gekommen!
wäre die hintere Seite senkrecht, könnte man die Höhe der Py nur sehr aufwändig , wenn überhaupt , ermitteln.
ich denke nun , da dies ja eine Fragewiederholung ist ,dass dieser rechte
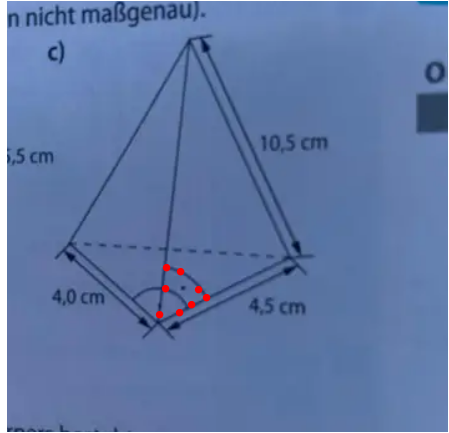
Winkel bedeuteten soll ,dass dessen Seite senkrecht steht :::::::::::::::::
Die Höhe der Py wäre also wurz(10.5² - 2.25²)
.
Weil die Grundfläche rechtwinklig ist , kann man deren Fläche mit
4*4.5/2 schnell bestimmen.
.
V = 1/3 * (4*4.5/2) * (10.5² - 2.25²)^0.5 =
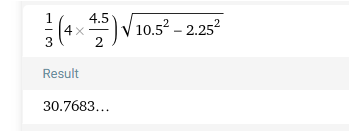
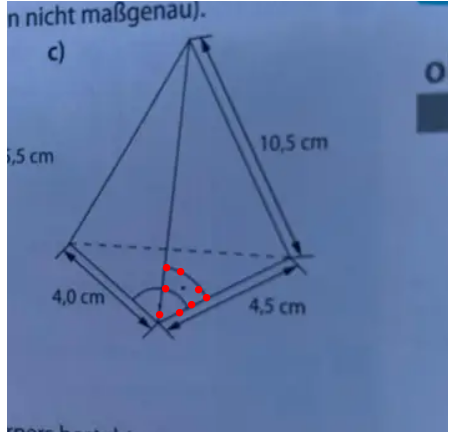
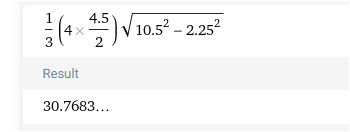
Welche Werte nehme ich denn für die 3 identischen Pyramiden? Eine Seite ist ja 4cm und die andere 4,5