Warum ist (x=1 oder x=-1) äquivalent zu x^2 = 1?
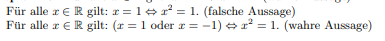
Ich verstehe irgendwie die Aussage nicht ganz.
Also wenn wir im x eine 1 einsetzen, kommt eine 1 raus, ja. Aber -1^2 ist doch -1 (?), warum ist es dann eine wahre Aussage? Und x = 1 <=> x^2 = 1 wiederum eine falsche Aussage?
4 Antworten
ja, -1^2 ist -1. Aber (-1)^2 = 1. Und wenn man in x^2 für x -1 einsetzt steht da (-1)^2.
x = 1 <=> x^2 = 1 wird durch das Gegenbeispiel x = -1 widerlegt. Es ist zwar die "=>" Richtung richtig, aber die "<=" Richtung falsch.
Der doppelpfeil sagt aus, dass aus dem einen das andere und auch aus dem anderen das eine zu schlussfolgern ist.
Bei 1)
Wenn x=1 dann ist x^2=1 ist eine wahr aussage, ABER wenn x^2=1 dann muss x nicht gleich 1 sein, sondern kann auch -1 sein.
2) bezieht den Fall mit ein. Es wird dabei nicht -1^2 sondern (-1)^2 gerechnet
Minus mal Minus ist Plus.
Also: (-1)2 = 1
Somit kann bei x2 = 1 auch -1 für x eingesetzt werden.
Die Lösungsmenge ist also sowohl 1 wie auch -1, nur die 2. Aussage ist wahr.
(-1)^2 = 1 und nicht -1.
Und x = 1 <=> x^2 = 1 ist eine falsche Aussage, denn x könnte ja auch -1 sein.