Verschobene normalparabel y=(x-d)hoch2?
Kann mir jemand die Aufgabe erklären wie zeichnet man ein Graphen mit den angegebenen Funktionswert

2 Antworten
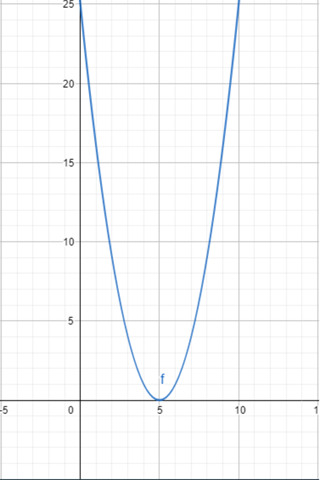
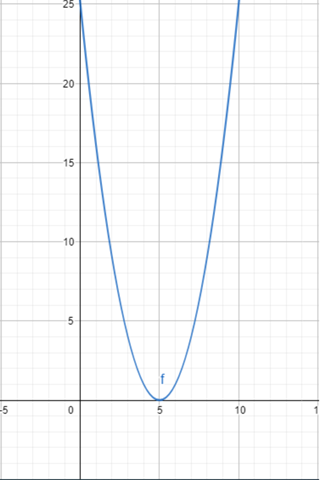
Für y = (x-5)² sieht das zum Beispiel so aus:
Es gibt da diese tolle Seite:
https://www.geogebra.org/calculator
Einfach mal ausprobieren!
y = (x - d)² + e
ist die Scheitelpunktform. Bei a -d ist e Null
y = (x - d)² + 0
Lies den Scheitelpunkt ab, markiere ihn im KS, setzt die Parabelschablone an (wenn du eine hast) und zeichne die Parabel. Alle P sind nach oben geöffnet und normal.
Du sollst ablesen, wo (x-Werte) die gezeichnete Parabel den Funktionswert (y-Wert) hat.
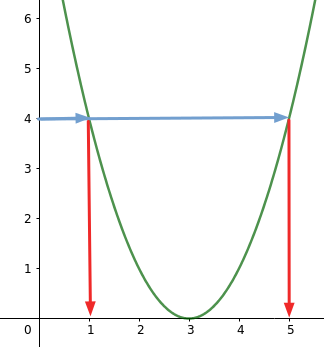
Bsp. mit y = (x- 3)² und Funktionswert 4:
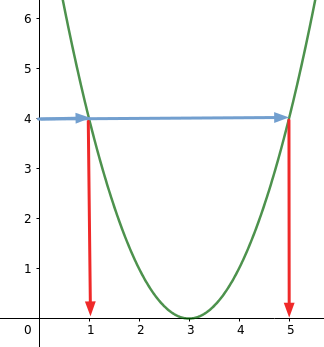
Du gehst von Funktionswert so lange wagerecht nach rechts oder links (Im Beispiel rechts), bis du auf die Parabel triffst (das kann zweimal, einmal oder keinmal sein), blaue Pfeile.
Von dort gehst du senkrecht zur x-Achse (rote Pfeile) und liest die x-Werte ab.