Verdünnung einer Säure pH-Wert?

Ich steh hier auf der Leitung, da ich von meinen Kollegen widersprüchliche Lösungswege vorgeschlagen bekomme.
Konkret geht es um die zweite Frage, nämlich wie verändert sich der pH-Wert wenn man 1ml der Lösung entnimmt und mit 99ml Wasser mischt. Am liebsten wär mir eine Lösung mit der Formel für die Berechnung von pH-Werten für schwache Säuren, nämlich diese hier :
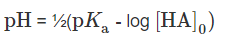
Kennt sich hier jemand damit aus?
1 Antwort
Du hast 900 mg ≙ n=m/M=0.01 mol Milchsäure in 250 ml Wasser gelöst, die Stoffmengenkonzentration beträgt also c=n/V=0.04 mol/l. Gefragt ist der pH-Wert, und wie der pH-Wert bei einer Verdünnung um den Faktor 100 aussieht. Der pKₐ-Wert von Milchsäure ist übrigens nicht einfach ≈4, sondern pKₐ=3.86 (steht im Internet).
Kurz zusammengefaßt: wie groß ist der pH-Wert einer Milchsäurelösung mit der Konzentration (a) 0.04 mo/l und (b) 0.0004 mol/l?
Um den pH-Wert einer wäßrigen Säurelösung zu berechnen, gibt es eine ganze Speisekarte von Formeln, die ich Dir hier in einer übersichtlichen Aufstellung präsentiere:

Kurz gesagt, muß man unterscheiden, ob die Säure stark, schwach oder dazwischen ist (das sind die Zeilen) und ob der pH-Wert allein von der Säure bestimmt wird oder auch das Wassergleichgewicht berücksichtigt werden muß (das sind die Spalten). Die Formeln in der letzten Zeile fasse die darüberliegeden zusammen, die Formeln in der zweiten Spalte beinhalten die erste — deshalb ist die Formel rechts unten immer anwendbar, ihre Ableitung habe ich kürzlich beschrieben.
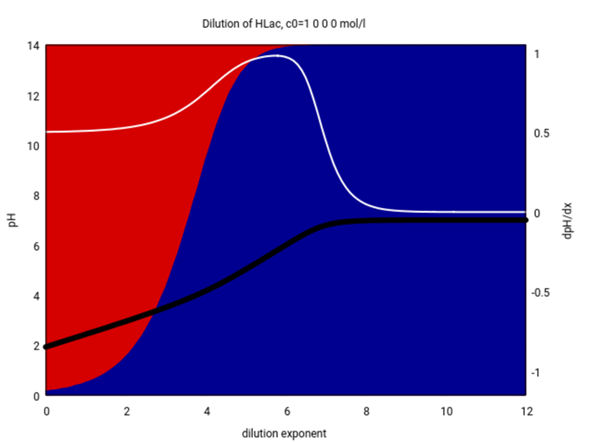
Man kann sich das auch als Plot ansehen und den pH in Abhängigkeit von der Konzentration plotten. Das siehst Du jetzt hier unten; die Hintergrundfarben geben die relativen Mengen freier Milchsäure und Lactat an. Die schwarze Kurve ist der pH, und die weiße die erste Ableitung davon:
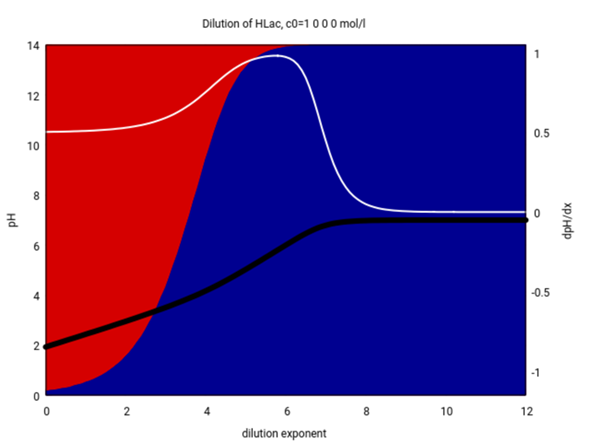
Uns interessieren die Konzentrationen 0.04 und 0.0004 mol/l, das sind 10⁻¹·⁴ bzw. 10⁻³·⁴ mol/l, also finden wir das bei den x-Werten 1.4 bzw. 3.4.
- Bei 0.04 mol/l liegt wirklich vorwiegend freie Milchsäure vor, die Säure kann also als schwach (= wenig dissoziiert) gelten. Mit der Formel pH=½(pKₐ−lg(c₀)) für schwache Säure bekommt man pH=2.63, und das ist so gut wie richtig (eine bessere Formel würde 2.63 liefern).
- Aber bei 0.0004 mol/l siehst Du, daß die Säure bereits stark dissoziiert ist. Mit derselben Formel wie zuvor bekämst Du pH=3.63, und das läßt alle Alarmklingeln schrillen, denn diese Formel gilt nur wenn die Säure schwach dissoziiert ist, also wenn pH≪pKₐ. Das ist nicht wirklich der Fall, deshalb müssen wir auf eine bessere Formel umsteigen, nämlich auf eine in der letzten Zeile (es reicht die linke, weil pH≪7). Wir rechnen den pKₐ in die Säurekonstante um Kₐ=10⁻ᵖᴷᵃ und bekommen pH=−lg [ √(¼Kₐ² + Kₐ⋅c₀) − ½Kₐ ] = 3.76, und das ist schon ein merklicher Unterschied — immerhin liegen 44% der Säure als Anion vor, und nur 56% als undissoziierte Säure.
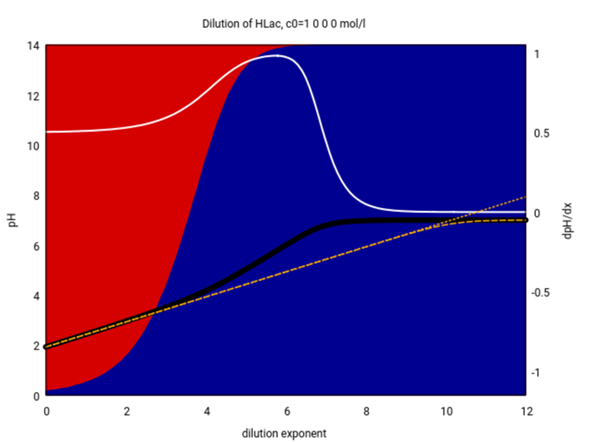
P.S.: Die folgende Graphik zeigt Dir, wie gut die Formel für schwache Säuren für Milchsäure funktioniert. Die Graphik ist dieselbe wie oben, aber zusätzlich habe ich noch die berechneten pH-Werte mit den Formeln für schwache Säuren eingezeichnet (die gepunktete ist die, die ich oben verwendet habe, und die strichlierte ist die, die noch zusätzlich das Wassergleichgewicht berücksichtigt; die beiden unterscheiiden sich nur bei extrem gerinngen Konzentrationen)
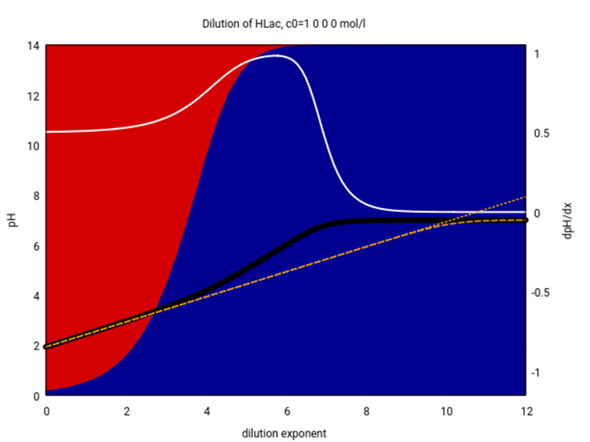
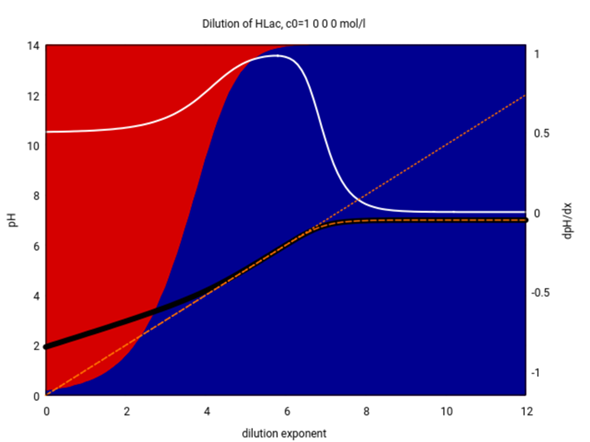
Die Formel für schwache Säuren ist also bis etwa 10⁻² mol/l verläßlich, beginnt aber bei weiterer Verdünnung immer mehr abzuweichen. Bei 10⁻⁴ mol/l und darunter ist sie definitiv unbrauchbar. Unterhalb von 10⁻⁵ mol/l könnte man bereits die Formel für starke Säuren pH=−lg(c₀) verwenden, die paßt dann nämlich sehr gut, und das zeige ich auch noch mal (bei ≈10⁻⁷ mol/l und darunter braucht man dann aber wirklich das Wassergleichgewicht zusätzlich):
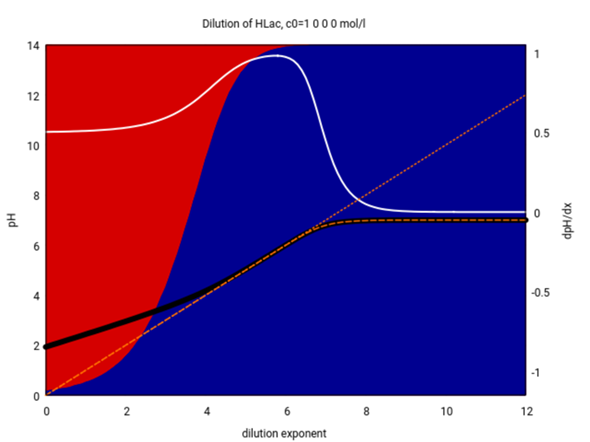

Meine Frage lautet jetzt, ob ich diese Verdünnung von 1:100 (Entnahme von 1ml und auf 100ml verdünnen) so berechnen kann (näherungsweise), dass ich statt der Konzentration 4*10^-2 einfach mit 4*10^-4 rechne.
Natürlich. Nur brauchst Du dann, falls Du eine realistische Zahl haben willst, eine andere Formel. Mit pKₐ=4 und c₀=0.04 kriegst Du pH=2.70, und das ist gut genug (genau 2.71). Bei c₀=0.0004 mol/l würdest Du 3.70 herausbekommen, und mit einer anständigen Formel 3.81.
(Wie rechnest Du den Logarithmus ohne Taschenrechner aus? Logarithmentafel?)
Bei einem anderen Beispiel, wo eine Base mit pKb von 6 und in einer Konzentration von 0,1 M vorgelegen ist, wurde 1ml entnommen und auf 1000ml verdünnt.
Da gehst Du im Prinzip gleich vor, pH=14−½[pKb−lg(c₀)]=10.50 für die Stammlösung und pH=9.00 für die Verdünnung. In diesem Fall sind beide Werte brauchbar; der pKb ist 6 und der pKₐ daher 14−pKb=8, da bist Du noch im sicheren Bereich (eine bessere Formel würde pH=8.98 ergeben, das ist vernachlässigbar).
Vielen, vielen Dank, das rettet meinen Tag. Ich war schon vollkommen frustriert, weil ich nur widersprüchliches dazu bekommen habe. Eine Frage hätte ich noch: Wenn ich den pOH-Wert einer (starken) Base berechne, wie z.B von Ba(OH)2 und ich das in die Formel -log[OH-] einsetze, muss ich ja den log mit 2 multiplizieren, weil ein mol Bariumhyrdoxid in zwei OH- Ionen dissoziiert. Ist das bei Basen wie H2SO4, H3PO4 etc. eigentlich auch so? Dass ich log[H3O+] dann mit 2 bzw. 3 multiplizieren muss?
Unser Vortragender erklärt leider nur sehr wenig und wirft uns bei der Prüfung dann alles hin. :/
Ein Problem habe ich auch mit folgendem Thema: https://www.gutefrage.net/frage/in-wie-viele-teilchen-zerfaellt-schwefelsaeure-aluminiumchlorid-bariumhydroxid-essigsaeure-wenn-man-genuegend-wasser-hinzufuegt
Dazu hat leider noch niemand geantwortet, vielleicht können Sie mir da auch weiterhelfen?
Logarithmieren mit Tafel, ja.
Danke :)
Ist das bei Basen wie H2SO4, H3PO4 etc. eigentlich auch so? Dass ich log[H3O+] dann mit 2 bzw. 3 multiplizieren muss?
Ba(OH)₂ ist stark, daher geht das. Die von Dir aufgezählten Säuren (nicht Basen!) sind aber leider komplizierter.
Bei der H₂SO₄ ist nur die erste Dissoziationsstufe stark, die zweite wird erst bei pH⪆2 aktiv; da braucht man also wieder spezielle Formeln. Wenn Du danach fragst, dann kann ich Dir noch eine Antwort schreiben.
Bei H₃PO₄ ist selbst die erste Dissoziationsstufe nur mittelstark. Die Formel für beliebige Säure fuktioniert fast über den ganzen Konzentratonsbereich, weil die zweite Dissoziationsstufe nur in extremer Verdünnung, wenn der pH schon fast 7 ist, zum Tragen kommt.
"Logarithmieren mit Tafel, ja."
Das ist ja reine Schikane. So hat man vor 50 Jahren gerechnet ...
Schikane wäre, wenn man das im Kopf rechnen müsste.
In der hier sinnvollen Genauigkeit wäre das aber auch kein Problem, wenn man die ungefähren Logarithmen für 2 und 3 im Kopf hat.
oder an geeigneter Stelle auf der Zunge des Rechenschiebers ...
Vielen Dank für die ausführliche Erklärung. Es geht allerdings nur um eine Klausur im Pharmaziestudium, bei der ich zu allem Überfluss *keinen* Taschenrechner verwenden darf.
Deswegen rechne ich diese Rechnung wie folgt:
Ich rechne mir das Molekulargewicht der Milchsäure aus, welches bei 90g/mol liegt.
Dann dividiere ich die 900mg/90, allerdings rechne ich mit mmol weiter, damit es einfacher ist.
900/90=10. Dann noch mit 4 multiplizieren, da ich ja mit der von mir genannten Formel auf Liter rechnen möchte.
c würde dann 40 mmol/l ergeben. Um den Logarithmus ohne Taschenrechner zu rechnen, schlüssle ich das ganze auf auf lg(4*10^-2) und rechne mir lg(4) und lg(10^-2) einzeln aus.
Wenn ich dann rechne 0,5*(pks-log(c)), dann komme ich ebenfalls auf einen pH-Wert von 2,7.
Meine Frage lautet jetzt, ob ich diese Verdünnung von 1:100 (Entnahme von 1ml und auf 100ml verdünnen) so berechnen kann (näherungsweise), dass ich statt der Konzentration 4*10^-2 einfach mit 4*10^-4 rechne.
Mit anderen Formeln kann ich aufgrund des Zeitmangels und des nicht vorhandenen Taschenrechners & das Nicht-Erlernen anderer Formeln nicht arbeiten.
Bei einem anderen Beispiel, wo eine Base mit pKb von 6 und in einer Konzentration von 0,1 M vorgelegen ist, wurde 1ml entnommen und auf 1000ml verdünnt. Die Lösung der Rechnung war wie folgt ->
c / 1000 = 0,0001M
Einsetzen in die Formel = pOH= 0,5* (6 - log (0,0001)) und am Ende für den pH-Wert natürlich noch 14-pOH.
Ich möchte nur wissen, ob ich das im oben genannten Fall mit der Milchsäure ebenfalls so rechnen kann.
Vielen Dank für die Hilfe.