van-der-Waals-Gleichung: wie zeigen, dass partielle Ableitungen gleich sind?
Hallo,
ich stehe gerade vor einem Problem. Ich muss beweisen, dass 2 partielle Ableitungen (siehe Anhang) gleich sind. Aber ich habe da echte Probleme. Kann mir Da jemand helfen?
Danke im Vorraus
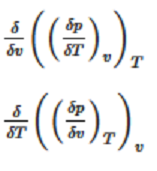
2 Antworten
Hallo,
ich verstehe das Problem so, dass die Vertauschbarkeit der 2-ten partiellen
Ableitungen festgestellt/bewiesen werden soll:
Gilt ∂/∂v ∂/∂T p = ∂/∂T ∂/∂v p oder ∂²/∂v∂T p = ∂²/∂T∂v p ?
(zwei Schreibweisen)
Der Satz von Schwarz besagt: sind die 2-ten partiellen Ableitungen in einer Umgebung eines Punktes noch stetig, dann kann man die Reihenfolge der partiellen Ableitungen vertauschen, das Ergebnis ist das gleiche.
https://de.wikipedia.org/wiki/Satz_von_Schwarz
Iich kenne jetzt den Zusammenhang deiner Aufgabe nicht (sie scheint aus der Physik zu kommen?), aber wenn ich das richtig verstanden habe, würde es mit Berufung auf den Satz genügen, die Stetigkeit der zweiten partiellen Ableitungen festzustellen, um auf die Gleichheit zu schließen.
Gruß
Da darf dann aber nicht V stehen, sondern Vm. Vm kannst du nicht einfach nach V ableiten. Setze für Vm=V/n ein und du kommst auf eine Form, die du ableiten kannst.
Ok, das sagt mir jetzt nichts - ist m ein Index, eine Konstante?
Ist Physik - dann bin ich lieber ruhig. Vielen Dank.
V ist das Volumen, Vm das molare Volumen. Also das Volumen pro "Teilchenanzahl".
Leite die VdW-Gleichung erst nach T ab, dann diese Ableitung nach V. Das gleiche machst du noch einmal andersherum.
Dann kannst du ja sehen, ob beide gleich sind.
Dann komme ich bei beiden auf -R/(b*v)^2
Kann das stimmen?
Ich muss für beide partiellen Ableitungen das Ergebnis aufschreiben. Also jeweils den Term