Uran-235 Halbwertszeit?
Hey!
Uran-235 hat eine Halbwertszeit von 703'800'000 Jahren. Nehmen wir an, wir haben 1000g Uran-235. Wie viel Uran-235 ist nach 200'000 Jahren noch vorhanden.
Kann mir dies bitte jemand anhand eines Lösungsweges, bestenfalls anhand einer Formel erklären?
Lg
Frageidee
2 Antworten
Wenn man zu Beginn eine gewisse Masse m₀ an Uran-235 hat und Uran-235 mit einer gewissen Halbwertszeit T zerfällt, so verbleibt nach Zerfallsgesetz nach einer gewissen Zeit t noch eine Masse
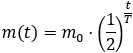
in Form von Uran-235. (Die restliche Masse ist zerfallen und befindet sich dann in anderer Form als Uran-235.)
Mit den konkret gegebenen Werten erhält man also ...
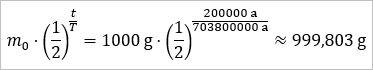
Es ist also zu erwarten, dass nach 200000 Jahren noch etwa 999,8 g des Uran-235 vorhanden sein werden.
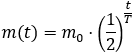
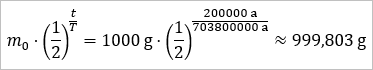
Du könntest beispielsweise hier schauen:
https://www.leifiphysik.de/kern-teilchenphysik/radioaktivitaet-einfuehrung/halbwertszeit
Da steht das Zerfallsgesetz in der Form ...
N(t) = (1/2)^(t/T) * N(0)
... wobei N die Anzahl der Kerne ist. Die Masse erhält man, indem man die Anzahl der Kerne mit der Masse eines einzelnen Kernes multipliziert. Wenn du die Gleichung also mit der Masse eines einzelnen Uran-235-Kerns multiplizierst, erhälst du das Zerfallsgesetz in der Form ...
m(t) = (1/2)^(t/T) * m(0)
============
In den meisten Quellen wirst du das Zerfallsgesetz bezogen auf die Anzahl N der Kerne oder bezogen auf die Aktivität A finden. Aber wie angegeben, erhält man die Masse durch Multiplikation der Kernanzahl mit der Kernmasse, weshalb das Zerfallsgesetz auch für die Masse an Uran-235-Kernen in einer Probe Gültigkeit hat.
============
Das Zerfallsgesetz wirst du übrigens in der ein oder anderen Form auch in den meisten physikalischen Formelsammlungen finden. (Du wirst doch bestimmt irgendwo eine Formelsammlung rumliegen haben, wenn du Physik als Fach hast. Schau doch mal was in deiner Formelsammlung dazu steht und benutze vielleicht diese als Quelle.)
Ich habe dir mal zwei Seiten aus Formelsammlungen eingescannt, in denen das Zerfallsgesetz in der Form N(t) = N₀ ⋅ (1/2)^(t/T) aufgeführt ist.
Andreas Gilg, Dr. Günter Rothmeier
Formelsamlung: Mathematik, Physik, Chemie
C.C. Buchners Verlag, Bamber, 1. Auflage 2009
https://i.imgur.com/Rj3TQYL.jpg
(Seite 98)
Sklarczyk, Thumann, Ramsteiner
Formeln und Gesetzmäßigkeiten: Mathematik - Physik - Chemie
Michael-Voll-Verlag, Druck: Böhler-Verlag, Würzburg, 1. Auflage 2007
https://i.imgur.com/rpqmDbN.jpg
(Seite 11 im Physik/Chemie-Teil)
Fußnote:
Die Formel für das Zerfallsgesetz ist gar nicht oft in der gut verständlichen Form zu finden, in der mihisu und Tannibi sie hier gezeigt haben. Aber hier steht sie so:
https://www.leifiphysik.de/kern-teilchenphysik/radioaktivitaet-einfuehrung/halbwertszeit (Am Ende des Abschnitts "Rechnerische Behandlung des radioaktiven Zerfalls")
https://en.wikipedia.org/wiki/Half-life (Am Anfang des Abschnitts "Formulas for half-life in exponential decay")
Danke jetzt versteh ich es. (-: Gibt es auch dazu eine Internetquelle wo dies geschrieben steht? Ich brauch dies nämlich für eine Arbeit und gutefrage.net eignet sich leider nicht als wissenschaftliche Quelle.