Unendlich ist keine Zahl: Warum darf man mit ∞ rechnen?
Warum darf man in der Mathematik mit ∞ rechnen?
∞ ist keine Zahl, sondern ein Konzept eines nie endenden Prozesses bei dem eine Zahl imaginär immer größer ist/wird als vorher.
Es ist keine klare Zahl und trotzdem heißt es, ∞+x=∞, obwohl richtiger wäre ∞+x=∞+x.
In der Formel dürften keine nicht klaren Konzepte stehen, weil es auch dem widerspricht, dass bei der Addition einer Zahl mit einer Zahl x>0 nicht wieder dieselbe Zahl als Ergebnis rauskommt. Das es bei ∞ so ist liegt daran, dass es keine Zahl ist.
Mit π kann auch nicht gerechnet werden, außer wenn π gerundet wird. Es ist ein Konzept einer immer präziser werdenden Zahl.
Es kann zwar zb aufgeschrieben werden: π·x=y aber wenn man y tatsächlich berechnen will, muss π gerundet werden.
Sollte man die Regel in der Mathematik korrigieren und die Regel einführen, dass mit ∞ nicht gerechnet werden kann.
Durch 0 darf man auch nicht teilen, sonst würde auch ∞ als Ergebnis rauskommen.
Warum darf man durch 0 nicht teilen, aber durch ∞ schon? Macht kein Sinn
12 Stimmen
6 Antworten
Hallo,
man darf mit unendlich nicht in dem Sinne rechnen, daß unendlich+unendlich=2*unendlich oder unendlich-unendlich=0.
Das funktioniert nicht. Man kann aber sagen, daß das Ergebnis einer Zahl ungleich Null, die durch unendlich geteilt wird, gegen Null geht oder daß 0,9999...999 mit unendlich vielen Neunen hinter dem Komma gleich 1 ist.
Unendlich tritt also da auf, wo es um Grenzwerte geht. Aber rechnen im klassischen Sinne geht damit nicht.
Und: Nein, man kann und soll hier auch keine mathematischen Regeln umschreiben.
Herzliche Grüße,
Willy
Vorab:
Ich denke, dass du ein vollkommen falschen Verständnis von unendlich großen Zahlen hast. Wenn du dich dafür interessierst dann würden dich transfinite Zahlen / transfinite Arithmetik und die Mengenlehre bestimmt begeistern.
Zudem verstehst du grundlegende Sachen über irrationale Zahlen nicht ganz.
Warum darf man in der Mathematik mit ∞ rechnen?
Da Arithmetik (siehe transfinite Arithmetik).
∞ ist keine Zahl, sondern ein Konzept eines nie endenden Prozesses bei dem eine Zahl imaginär immer größer ist/wird als vorher.
Nein.
Lassen wir den Punkt mit den Prozess weg beschreibst du die absolute Unendlichkeit (siehe transfinite Zahlen).
Es ist keine klare Zahl
Naja. Mit "∞" ist nicht klar welche Unendlichkeit gemeint ist, dennoch ist eine klare aka scharfe Zahl. Andern Falls wäre es eine Fuzzy Zahl (in duetschen öfters unscharfe Zahlen genannt), was sie aber nicht ist, da sie nur einen bestimmten Wert haben kann.
trotzdem heißt es, ∞+x=∞, obwohl richtiger wäre ∞+x=∞+x.
Ist x reell, dann sind beide Gleichungen für die absolute Unendlichkeit richtig, aber für transfinite x hast du natürlich recht.
In der Formel dürften keine nicht klaren Konzepte stehen, weil es auch dem widerspricht, dass bei der Addition einer Zahl mit einer Zahl x>0 nicht wieder dieselbe Zahl als Ergebnis rauskommt.
Das stimmt nicht. Das immer wieder das gleiche raus kommt nennt man bei Folgen auch absolute Konvergenz und ist ein wichtiges Konzept der Mathematik, hingegen zur Unendlichkeit. Das kannst du auch schnell bei Grenzwert-Betrachtungen finden.
Unklare Konzepte stehen auch in der Regel nicht in einer Gleichung, wie hier auch nicht.
Mit π kann auch nicht gerechnet werden, außer wenn π gerundet wird. Es ist ein Konzept einer immer präziser werdenden Zahl.
Es kann zwar z.B. aufgeschrieben werden: π·x=y aber wenn man y tatsächlich berechnen will, muss π gerundet werden.
Natürlich geht das:
π - π = 0
π^0 = 0
π^1 = π
sin(π) = 0
cos(π) = -1
exp(π i) = -1
Auch bei nicht so degenerierten Fällen geht das.
Du kannst sie nur nicht als Quotient zweier ganzer Zahlen darstellen.
Es gibt aber viele andere Darstellungsmöglichkeiten, wie z.B. durch geometrische Reihen z.B.
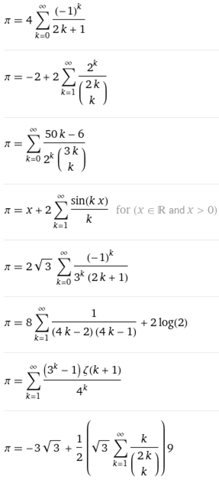
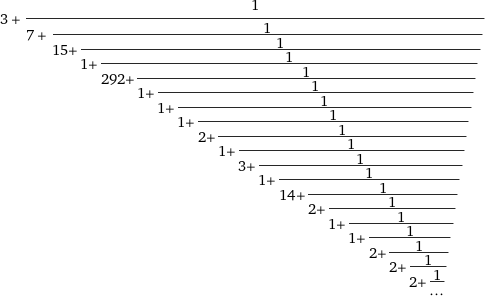
als Kettenbruch
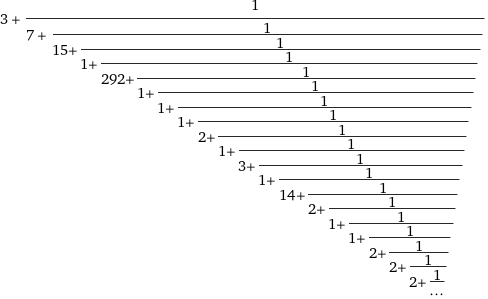
oder Funktionen
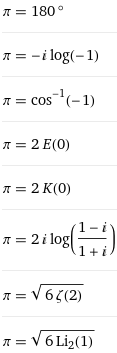
Sie sind alle eindeutig, scharf und ganz besonders ist pi kein Konzept, sondern eine irrationale Zahl.
Sollte man die Regel in der Mathematik korrigieren und die Regel einführen, dass mit ∞ nicht gerechnet werden kann.
Nein aber man sollte mal mehr und qualitativ hochwertigere Mathematik in der Schule lehren.
Durch 0 darf man auch nicht teilen, sonst würde auch ∞ als Ergebnis rauskommen. Warum darf man durch 0 nicht teilen, aber durch ∞ schon?
Nein. Nicht auch nur annährend.
Durch Axiome gilt unser Distributivgesetz. Würden wir durch 0 teilen können, wäre das Distributivgesetz nicht wahr, was ein Wiederspruch ist, also geht es nicht.
Es gilt nur:
und bei beiden Teilt man nicht durch 0.
Man kann viele Zahlen durch transfinite Zahlen teilen, weil für die meisten Zahlen keine Wiedersprüche auftauchen.
Macht kein Sinn
Macht zu 100% sinn, ansonsten wäre vieles in der modernen Physik und Mathematik falsch.
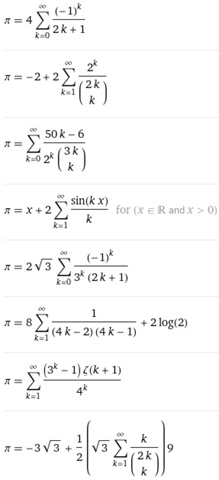
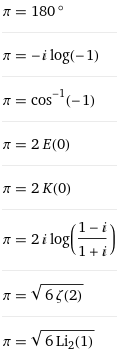
Ich versuche auf alles zu Antworten:
Dass man mit 0 multiplizieren kann, aber nicht durch 0 teilen darf ist aber auch ein Widerspruch zu den Umstellungsregeln.
Diese "Umstellregeln" existieren so per se nicht. Sie sind nur Konsequenzen aus den Axiomen. Die Axiome sagen nicht, dass man durch 0 teilen darf bzw. nicht das jede Operation für jede Zahl umkehrbar ist, wodurch der Fakt dass man nicht durch 0 teilen kann auch nicht "den Regeln" der Mathematik widerspricht.
Man betrachtet nicht die Unendlichkeit sondern die ständige Annäherung zum Unendlichen, nicht zu einem bestimmten Wert.
Man betrachtet tatsächlich genau eine Unendlichkeit. Ähnlich wie in der Infinitesimalrechnung. Wenn dir die Infinitesimalrechnung verständlicher ist kannst du dir transfinite Zahlen auch als eine Art Umweg von Algebra zur Analysis denken.
In der Realität würde so ein Vorgang sich tatsächlich nur der Unendlichkeit annähern.
Jede Zahl ist ein Konzept.
Ich glaube, dass wir da verschiedene Definitionen von Konzept nutzen.
Man könnte das aber anders lösen: 0 als keine Zahl mehr betrachten/multiplizieren verbieten oder teilen durch 0 erlauben. So einfach würde es gehen, und keine Regel hätte sich widersprochen.
Man erlaubt in der Mathematik so gesehen nichts. Man beurteilt nur ob es logisch ist oder sich widerspricht. Teilen durch 0 kann man leider nicht "erlauben", da man sich sonst damit herleiten könnte dass alle Zahlen gleich wären und somit nichts mit Zahlen in der Mathematik noch eine wirkliche Verwendung hätte, da es den Axiomen widerspricht.
Es macht nur dann Sinn, wenn man die Regeln nach denen Mathematik funktioniert bereits vorher festlegt. Mathematik besteht aus Axiomen, die sich nicht widersprechen dürfen, aber das heißt nur, dass Mathematik ein Konstrukt aus festgelegten Regeln besteht, was Logik bedeutet.
Sie dürfen sich widersprechen in einen Axiomsystem. Diese Systeme können sehr interessante Eigenschaften aufwerfen. Nur "Rechnen" macht in denen nicht mehr 100% Sinn.
Axiome wie: 0 ist eine Zahl, mit 0 darf man multiplizieren, mit irrationalen Zahlen kann man rechnen, ...
Axiome sind eher Mengentheoretisch formuliert in Formeln (siehe Logik), z.B.:
die Peano Axiome
Aber was wäre denn in der Physik falsch?
Ich habe nicht so viel mit Physik am Hut. Das steht halt nur häufig da.
Eine schnelle google-Suche hat ergeben:
- Theorie der unendlichen elektrischen Netzwerke seit Jahrzehnten
doch eine allgemeinere Antwort wäre wohl:
alles was mit Infinitesimalrechnung zu tun hat.
Es ist eine direkte Beziehung zwischen transfiniten Zahlen und Infinitesimalzahlen feststellbar, welche bedeuten würde, dass wenn es falsch ist auch alles mit Infinitesimalrechnung falsch wäre, worauf sich ODEs, PDEs, Bewegungssyteme, Beschreiben sich verändernder Systeme, ... beruht, was ziemlich wichtig ist für z.B. die Berechnungen von Geschwindigkeiten, Temperaturen, Massen, ... "absolut allem".
Die Vereinfachung aufs absolute Minimum ist dann nicht mehr nötig, dementsprechende Monster sind dann aber auch die Formeln.
Diese "Umstellregeln" existieren so per se nicht. Sie sind nur Konsequenzen aus den Axiomen.Die Axiome stellen die Regeln dar für das Umstellen. Und wenn die Umstellung eine Folge von den Axiomen ist, baut es auf diesen Regeln auf. Wenn es Ausnahmen gibt bei der Umstellung, sind die Regeln nicht konsistent.
Nicht mathematisch ausgedrückt:
• 0 ist eine natürliche Zahl
• alle natürlichen Zahlen darf man umstellen, außer der 0
0 soll damit zugleich in die gleiche Kategorie wie die anderen natürlichen Zahlen gehören, aber bei der Division nicht gleich behandelt werden. Die beiden Axiome widersprechen sich.
Lösung: 0 ist als keine Zahl mehr zu betrachten
Teilen durch 0 kann man leider nicht "erlauben", da man sich sonst damit herleiten könnte dass alle Zahlen gleich wären
"Peano betrachtete ursprünglich 1 als kleinste natürliche Zahl. In seiner späteren Version der Axiome, die im Folgenden modern notiert sind, ersetzte er 1 durch 0"
Man könnte sowohl teilen als auch multiplizieren, addieren und subtrahieren verbieten. Oder zumindest multiplizieren und dividieren. Die 0 als eine Nichtexistenz einer Zahl betrachten. Somit muss dann eine Zahl größer als 0 sein. x-x wäre dann Nichtexistenz einer Zahl welche mit 0 symbolisiert werden kann, jedoch keine Zahl ist. Dies würde mit den Axiomen der Umstellung übereinstimmen.
Mathematik ist auf Regeln aufgebaut. Die Regeln kann man alle ändern, solange sie sich gegenseitig nicht widersprechen und damit eine Logik haben, außer in einem "Axiomsystem".
Es ist eine direkte Beziehung zwischen transfiniten Zahlen und Infinitesimalzahlen feststellbar, welche bedeuten würde, dass wenn es falsch ist auch alles mit Infinitesimalrechnung falsch wäre
Wieso sollte das nicht sein können. Diese Möglichkeit kann man auch in Erwägung ziehen.
worauf sich ODEs, PDEs, Bewegungssyteme, Beschreiben sich verändernder Systeme
Wenn es um einen idealen Zustand geht, eine bestimmte idealisierte Modellvorstellung.
Beschreibungen von Systemen sind Beschreibungen von Modellen der tatsächlichen Realität.
Unendlichkeit wird in der Physik nicht als reale physikalische Größe verstanden, sondern als Hilfsmittel um Grenzwerte und Idealisierungen zu beschreiben, also nur theoretisch.
Beispiele:
• Unendlicher Wert des Gravitationsfeldes um eine punktförmige Masse bei einem Abstand null.
• Singularitäten als unendlich dichte und unendlich kleine Objekte zu beschrieben.
• Lichtgeschwindigkeit als Grenzwert für die Geschwindigkeit von Objekten mit Masse.
• Unendliche Reihen um elektromagnetische Felder oder quantenmechanische Wellenfunktionen zu beschreiben.
• Unendliches Potential in der Quantenmechanik, wenn man ein Teilchen in einem unendlich hohen Potentialtopf betrachtet.
Es ist keine klare Zahl und trotzdem heißt es, ∞+x=∞
Es ist keine Rechnung, sondern eine Konvention um das Ergebnis von Grenzwerten schneller bestimmen zu können.
∞+x=∞
Bedeutet, dass wenn man eine Folge a_n hat, die gegen unendlich geht und b_n die gegen eine konstante geht, dass dann die Summe gegen unendlich geht.
Mit π kann auch nicht gerechnet werden, außer wenn π gerundet wird.
In theoretischer Sicht kann damit berechnet werden, für die Theorie ist vollkommen irrelevant, dass ein Mensch es nicht per Hand hinbekommt.
Durch 0 darf man auch nicht teilen,
Nein, man darf durch 0 nicht teilen, weil sonst die Axiome der Reellen Zahlen verletzt werden.
Es gibt andere Zahlenstrukturen, wo die Division durch 0 und durch unendlich erlaubt sind. Zum Beispiel die Riemannsche Zahlenkugel. In den Reellen Zahlen geht das jedoch nicht, da ist vor allem unendlich keine Zahl, sondern eher eine Bezeichnung für eine Eigenschaft.
Es ist nicht deine Aufgabe und auch nicht meine an mathematischen Regeln etwas zu ändern. Der Weg der Mathematik zum "Unendlichen" war ein langer und steiniger, bei dem viele Fallen entschärft und auch viele Konflikte gelöst werden mußten. Wenn du wirklich Interesse am Thema hast empfehle ich dir
dort wird die Geschichte des Umgangs mit dem Unendlichen auf die Heuser eigene heitere und lockere, aber mathematisch stets exakte, Art beschrieben.
Deine Ausführungen zeigen ein grundsätzliches Unverständnis zum Thema höhere Mathematik, es würde zu weit führen dies hier alles auszuführen.
Wenn man zu einer unendlich großen Menge eine endliche Zahl addiert, bleibt die Menge immer noch unendlich groß, und es ändert sich nichts an der Unendlichkeit der Menge.
Daher stimmt ∞+x=∞
Ja, wollte mich aber nur zu der Unendlichkeit äußern. Macht meine Antwort ja nicht falsch, falls du das jetzt behaupten willst.
∞+x=∞
Macht meine Antwort ja nicht falsch
Doch vielleicht. Beweise dass ∞+x=∞ und nicht ∞+x=∞+x
Habe ich dir als Antwort bereits geschrieben, warum ∞+x=∞ ist. Oder hast du die nicht gelesen?
Ich denke, dass du ein vollkommen falschen Verständnis von unendlich großen Zahlen hast.Das kann sein, dass ich der Mathematik widerspreche, weil mich Unendlichkeit eher aus philosophischer Sicht interessiert als mathematischer. Und aus dieser ist "Konzept eines nie endenden Prozesses bei dem eine Zahl imaginär immer größer ist/wird als vorher" eine mögliche Definition. Es kann auch als Unendlichkeit als eine Absolute Eigenschaft betrachtet werden. Ohne klares bestimmtes definierbares Ende oder Begrenzung, ohne Wert, ohne die Möglichkeit der vollständigen Erfassung, sich selbst übersteigend.
Unendliches Universum: Unbegrenzt, ohne Rand, allesseiend, total, alleinig
Mit "∞" ist nicht klar welche Unendlichkeit gemeint ist, dennoch ist eine klare aka scharfe Zahl. da sie nur einen bestimmten Wert haben kann.Wie kann ein unendlicher Wert ein klarer bestimmter Wert sein?
Ein Konzept der Unendlichkeit kann klar sein, aber nicht die Unendlichkeit selber als ein klarer Wert. Die Darstellung mit dem Symbol ∞ kann klar sein und die Vorstellung was Unendlichkeit ist kann klar und bestimmt sein, aber das sagt nicht über die eigentliche Unendlichkeit aus. Dasselbe für irrationale Zahlen. ∞ ist nur ein Symbol, das auf die Eigenschaften hinweist, aber an sich nichts darüber aussagt.
dass bei der Addition einer Zahl mit einer Zahl x>0 nicht wieder dieselbe Zahl als Ergebnis rauskommtDas stimmt, weil das Ergebnis sich um x>0 unterscheiden muss. Zwei gleiche Zahlen haben einen einen Unterschied von x=0 bzw keinen Unterschied. Man betrachtet nicht die Unendlichkeit sondern die ständige Annäherung zum Unendlichen, nicht zu einem bestimmten Wert.
π - π = 0
Das zu sagen ist ein Axiom, aber tatsächlich dürfte man es nicht, weil es unter die selbe Kathegorie wie ∞-∞=0 fallen würde, da eine Unendlichkeit nach Komma. Wenn man logisch denkt außerhalb mathematischer Regeln/Axiome. Rechnung mit π ist Rechnung mit Unendlichkeit.
Es gibt aber viele andere Darstellungsmöglichkeiten Richtig, aber darstellen bedeutet nichts, weil die Darstellung ein ∞ benutzt wird über dem Sigma, beim Kettenbruch kommt man nie zum Ende. Ich kann nach demselben Prinzip auch Unendlich darstellen: ∞ , 1+1+1+1+1...
Sie sind alle eindeutig, scharf und ganz besonders ist pi kein Konzept, sondern eine irrationale Zahl. Jede Zahl ist ein Konzept.
Eindeutig dargestellt, nicht eindeutig seiend. π ist nicht eindeutig
Würden wir durch 0 teilen können, wäre das Distributivgesetz nicht wahr, was ein Wiederspruch ist, also geht es nicht. Dass man mit 0 multiplizieren kann, aber nicht durch 0 teilen darf ist aber auch ein Widerspruch zu den Umstellungsregeln. Mathematik hat diesen Widerspruch, weil sich die festgelegten Regeln widersprechen. Deshalb wird teilen durch 0 nicht definiert. Weil es ein Widerspruch ist. Man setzt die Regeln bei der Umstellung außer Kraft bei diesem Fall, weil man dazu gezwungen ist. Mit anderen Worten setzt man die Logik außer Kraft bei 0. Man könnte das aber anders lösen: 0 als keine Zahl mehr betrachten/multiplizieren verbieten oder teilen durch 0 erlauben. So einfach würde es gehen, und keine Regel hätte sich widersprochen.
Macht zu 100% sinn
Es macht nur dann Sinn, wenn man die Regeln nach denen Mathematik funktioniert bereits vorher festlegt. Mathematik besteht aus Axiomen, die sich nicht widersprechen dürfen, aber das heißt nur, dass Mathematik ein Konstrukt aus festgelegten Regeln besteht, was Logik bedeutet.
Axiome wie: 0 ist eine Zahl, mit 0 darf man multiplizieren, mit irrationalen Zahlen kann man rechnen, ...
ansonsten wäre vieles in der modernen Physik und Mathematik falsch.
In der Mathematik ja. Aber Mathematik ist auch keine Wahrheit, sondern ein menschliches Konstrukt, eine Sprache, eine Erfindung. Sprache hat auch Regeln, Grammatik und Bedeutung. Aber was wäre denn in der Physik falsch? Mathematik ist ein Konzept, welches nicht unbedingt was mit der Realität und Physik zu tun haben muss und abhängig davon funktioniert. In der Physik wird Mathematik zu Berechnungen und Beschreibungen verwendet, nur weil man physikalische Beobachtungen auf das Minimum vereinfacht. Es gibt nichts in der Physik was 1 oder 2 entsprechen würde, oder exakt 2, weil Mathematik eine Sprache ist, und genau wie alle anderen Sprachen mit Wörtern die Realität vereinfacht beschreiben als ein Konstrukt, nur dass statt den Wörtern Formeln und Zahlen verwendet werden. Es ist nichts Weiteres, außer dass es wegen den vielen festgelegten Regeln diese eingehalten werden müssen, und die Logik dabei wichtiger ist. Wenn diese Regeln eingehalten werden, ist eine mathematische Aussage richtig. Wenn diese Regeln gebrochen werden, ist eine mathematische Aussage falsch.