Trapez Aufgaben 11 Klasse?
Hi Leute ich habe wirklich Probleme mit diesen beiden Übungen und ich muss sie bis morgen fertig haben, also wäre ich dankbar für Hilfe bei mindestens einer 🥲🥲
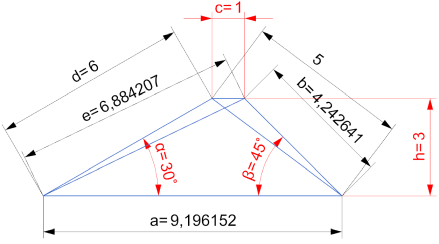
Die kürzere Basis des Trapezes ist 1 cm lang und die Höhe des Trapezes beträgt 3 cm. Berechnen Sie, dass die Winkel an der unteren Basis 30° und 45° betragen:
(a) den Umfang des Trapezes
(b) die Längen der Diagonalen des Trapezes.
oder
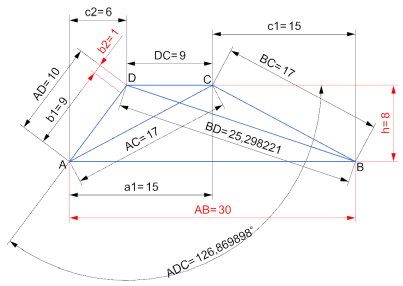
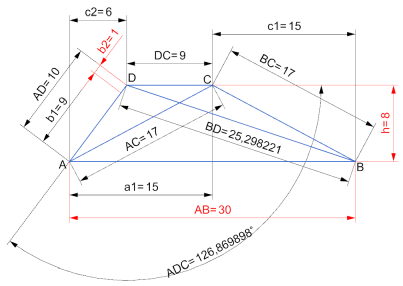
Die Höhe des Trapezes ABCD beträgt 8 cm und die Grundfläche AB ist 30 cm lang. Der Schenkel AD ist 1 cm länger als die Grundfläche DC. Berechnen Sie, dass die Diagonale AC und der Schenkel BC gleich lang sind:
A) den Umfang des Trapezes ABCD
b) die Länge der Diagonale BD
c) den Sinus des Winkels ADC.
danke!!!!
1 Antwort
Aufgabe 1
b = h / sin(β)
b = 3 / sin(45)
b = 4,242641 cm
---
a = (h * tan(β)) + c + (h * tan(α))
a = (3 * tan(45)) + 1 + (3 * tan(30))
a = 9,196152 cm
---
d = h / sin(α)
d = 3 / sin(30)
d = 6 cm
---
Diagnonale e berechnen
e = Wurzel( a² + b² - 2 * a * b * cos(β) 9
e = Wurzel(9,196152^2 + 4,242641^2 - 2 * 9,196152 * 4,242641 * cos(45))
e = 6,884206 cm
---
Diagnonale f berechnen
f = Wurzel( (a² + d²) - (2 * a * d * cos(α))
f = Wurzel( (9,196152^2 + 6^2) - (2 * 9,196152 * 6 * cos(30)) )
f = 5 cm
---
Umfang berechnen
U = a + b + c + d
U = 9,196152 + 4,242641 + 1 + 6
U = 20,438793 cm
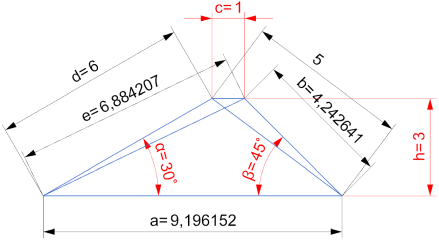
Aufgabe 2
BC = Wurzel( (AB / 2)² + h² )
BC = Wurzel( (30 / 2)^2 + 8^2 )
BC = 17 cm
---
AC = BC
AC = 17 cm
---
c1 = Wurzel(BC² - h²)
c1 = Wurzel(17^2 - 8^2)
c1 = 15 cm
---
DC = (a1² + h² - b2²) / ((a1 * 2) + (b2 * 2))
DC = (15^2 + 8^2 - 1^2) / ((15 * 2) + (1 * 2))
DC = 9 cm
---
AD = DC + 1
AD = 9 + 1
AD = 10 cm
---
c2 = AB - c1 - DC
c2 = 30 - 15 - 9
c2 = 6 cm
---
AD = Wurzel(h² + c2²)
AD = Wurzel(8^2 + 6^2)
AD = 10 cm
---
Umfang berechnen
U = AB + BC + DC + AD
U = 30 + 17 + 9 + 10
U = 66 cm
---
Diagnonale BD berechnen
BD = Wurzel( (AB² + AD²) - (2 * AB * AD * (c2 / AD)))
BD = Wurzel( (30^2 + 10^2) - (2 * 30 * 10 * (6 / 10)))
BD = 25,298221 cm
---
Winkel(ADC) = ARCCOS( (AC² - DC² - AD²) / (-2 * DC * AD) )
Winkel(ADC) = ARCCOS( (17^2 - 9^2 - 10^2) / (-2 * 9 * 10) )
Winkel(ADC) = 126,869898°
---
Sinus des Winkels ADC
sin(ADC) = sin(126,869898)
sin(ADC) = 0,8