Totales Differential berechnen und prüfen?
Hallo,
un

d zwar geht es um folgende Aufgabe.
Wie man ein totales Differential aufstellt, kein Problem.
Wie man prüft ob ein totales differenzial vorliegt, auch kein Problem.
Was man nicht lernt, was ist es wenn es kein totales differenzial ist, bzw was sagt mir das aus.
In der Aufgabenstellung sieht man, dass man mit dem totalen Differential rechnen soll. Wie man das bekommt garkein Problem, wenn ich jetzt aber dieses besagte Differential prüfe, auf ein totales Differential, indem ich die zweiten gemischten Ableitungen bilde, dann sehe ich, dass es laut Satz von Schwarz kein totales Differential ist, da die Ableitungen nicht gleich sind....
Das wiederum widerspricht ja aber der Aufgabenstellung, indem ich das totale Differential anwenden soll...
Wo liegt hier der Fehler?
Danke im Voraus
2 Antworten
Wenn du eine Funktion gegeben hast und ihr totales Differential berechnest, muss es auch ein totales Differential sein. Wenn der Check mittels zweiten Ableitungen was anderes aussagt, hast du dich entweder bei der Berechnung des totalen Differentials oder beim Berechnen der zweiten Ableitungen vertan.
Ein Ausdruck der Form a(x,y)*dx + b(x,y)*dy ist nur dann kein totales Differential, wenn keine Funktion z(x,y) existiert, sodass a = dz/dx und b = dz/dy. Dir ist aber genau diese Funktion z gegeben.
Und hier sieht man ja am Ende minus mal minus ...
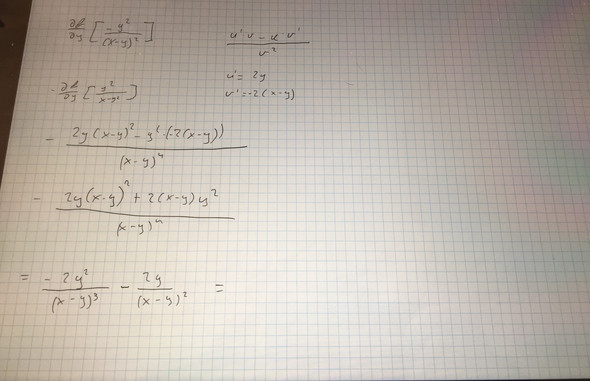
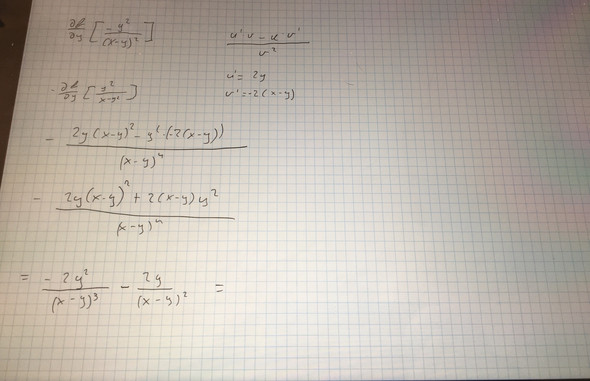
Schaut doch gut aus, jetzt bringe beide Terme auf den gleichen Nenner und vereinfache.
danke dir! aber es ist ja eine Lösung aus dem buch....-y^2/(x-y)^2 und x^2/(x-y)^2 haben ja nicht dieselbe gemischte 2 Ableitung ....