Textaufgabe Flächenberechnung?
Hi, hat jemand die Textaufgabe „Eine Grundstücksänderung“ (s. Bild) aus dem Mathebuch „Mathematik neue Wege 9“ für Nordrhein-Westfalen, Hamburg und Bremen schon mal gelöst und könnte mir die Lösung schicken? Das wäre sehr lieb!

3 Antworten
Ich würde mit der gelben Fläche rechnen.
Das wäre ja: 1000 - 156 = 844 m²
Und folgende Gleichung verwenden.
(40 - x) * (25 - x) = 844
x wäre die Breite der Straßen.
---
(40 - x) * (25 - x) = 844
x² - ((40 + 25) * x) + (40 * 25) = 844
x² - 65x + 1000 = 844
x² - 65x = -156
x² - 65x + (-(65/2))² = (-(65/2))² - 156
x² - 65x + (-(65/2))² = (4225/4) - 156
x² - 65x + (-(65/2))² = (4225/4) - (624 / 4)
x² - 65x + (-(65/2))² = 3601/4
(x - (65/2))² = 3601/4
(x - (32,5))² = 900,25
---
x - (65/2) = -Wurzel(3601/4)
x - 32,5 = -Wurzel(900,25)
x - 32,5 = -30,004166377355
x = 2,49583362264501 m

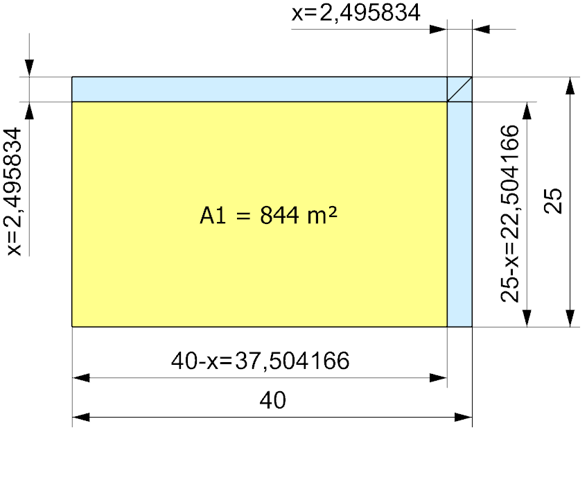
40*x (Fläche oben) + 25 * x (Fläche rechts) - x*x (Überlappung, die zweimal vorkommt) = 156
40x + 25x - x^2 = 156
-x^2 + 65x = 156
Nach 0 umstellen und dann mit Mitternachtsformel lösen
Wie lautet denn das Ergebnis am Ende. Bei mir geht die Gleichung nicht auf. Es kommt30.00416666 bei der Wurzel raus. Setze ich in der Probe 30 ein, erhalte ich 156,25. Wo ist der Fehler?
Es würde mich freuen wenn mir einer von euch beiden die weitere Rechnung und Lösung mal hier aufschreiben würde.
Die Fläche des blauen Streifens beträgt: 40*x + 25*x - x*x
Das soll 156 ergeben: 40*x + 25*x - x*x = 156
Umstellen: x² - 65*x + 156 = 0
Lösung:
x1 = 65/2 - sqrt(3601/4) ~ 2.4958
x2 = 65/2 + sqrt(3601/4) ~ 62.502
Die Lösung x2 entfällt, weil die Grösse des gelben Grundstücks überschritten wird.
Man darf aber nicht 65 zum Quadrat hinzuzählen, sondern nur 32,5 ². So ist meine Lösung nicht ganz falsch, aber nur annähernd richtig. Was für die Praxis ja ok wäre.
25x + 40x -x²= 156 mal -(1) und sortiert / Plus 32,5²
x² + 65 x +32,5² = -156 + 32,5²
(x - 32,5)² = - 156 + 1056,25 | Wurzel ziehen
x - 32,5 = Wurzel aus 900,25
x -32,5 = + / - 30,004166
x1 = ungefähr 2,5
x 2 kommmt aufgrund der Sachlage nicht in Frage.
Bei der pq-Formel kommt natürlich das Gleiche raus.
Der Fehler bei der Probe entsteht, weil der gerundete Teil nicht berücksichtigt wird. Danke für die Aufgabe und eure Hilfe.
65 wird nicht zum Quadrat hinzugezählt, sondern nur 40*x + 25*x = 65*x
Mitternachtsformel hatten wir leider noch nicht.