Teilmenge, echte Teilmenge, Gleichheit?
Angenommen es gibt eine Menge A und eine Menge B und Menge A hat genau die gleichen Elemente wie B. Wieso ist A dann eine Teilmenge von B? Warum gibt es die Teilmenge überhaupt, wenn es doch dasselbe wie die Gleichheit ist? Statt Teilmenge kann man doch gleich A=B schreiben oder nicht? Und woher weiß man was die Teilmenge von welcher Menge ist, wenn sie doch eh gleich sind?
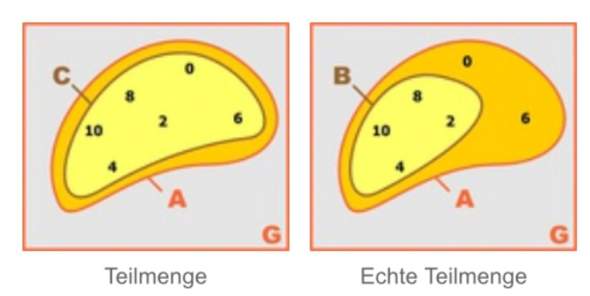
Solche Darstellungen verwirren mich:
1 Antwort
Links ist A = C. Damit ist A Teilmenge von C und gleichzeitig C Teilmenge von A.
Rechts ist B Teilmenge von A aber ist gibt Elemente in A, die nicht in B liegen. Daher ist A nicht Teilmenge von B. Man sagt dann, dass B echte Teilmenge von A ist.
Wenn man es von vornherein weiß, wird man das wohl auch so machen.
In komplizierteren Fällen stellt sich die Gleichheit aber eventuell später heraus.
keine ahnung was du genau meinst, aber beides hat seinen sinn. es ist wie mit echt kleiner und kleiner gleich.
teilmenge ist nicht das selbe wie gleichheit
A teilmenge von B heißt, dass A nur elemente von B haben kann, aber nicht mehr.
A echte Teilmenge von B heißt, dass A nur elemente von B haben kann, aber nicht alle.
ungefähr verstanden?
wenn man zeigen will, dass zwei mengen A und Bgleich sind, dann zeigt man meistens dass A teilmenge von B ist UND B Teilmenge von A ist. dann gilt offensichtlich A=B
Wann ist etwas nur Teilmenge ohne dass Gleichheit ebenfalls zu trifft?
Das ist dann eine echte Teilmenge. (wie im rechten Bild)
Aber wieso nutzt man nicht nur echte Teilmengen und Gleichheit wenn die Teilmenge sowieso dasselbe wie Gleichheit ist?