Vollständige Inudktion über größer gleich >=?
Zu beweisen

Wenn ich das mithilfe der Induktion über n machen möchte (erstes Element von N ist 1) und dadurch beim Induktionsanfang herauskommt, dass 1+x=1+x
Aber wenn ich jetzt den Induktionsschritt mache, und dieselbe aussage für n+1 beweisen möchte, komme ich statt größer gleich auf echt größer.
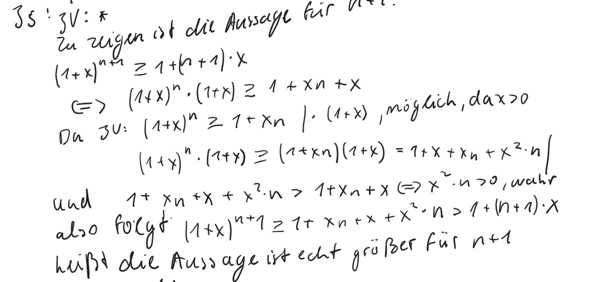
Aber damit habe ich doch nicht die Aussage für n+1 gezeigt? Denn für n+1 ist sie ja echt gleich.
kann ich jetzt sagen: da für n=1 die gleichheit gilt und für n+1 die ungleichheit, dass somit folgt, dass (1+x)^n >= 1+nx, weil man die gleichheit und die echt größer hat?
2 Antworten
Wenn etwas echt größer ist, dann ist es insbesondere auch größer gleich. Anders gesagt: Für alle Zahlen x, für die gilt
x > y
gilt natürlich auch
x ≥ y.
Insofern ist das völlig in Ordnung so, wenn du echt größer gezeigt hast, dann hast du auch größer gleich gezeigt - andersherum wäre das ein Problem, so rum aber nicht.
Darum gilt es ja andersherum auch nicht.
Echt größer ist eine schärfere Bedingung als größergleich. Wenn ich z. B. frage: Welche natürlichen Zahlen sind echt größer als 10, dann sind das die Zahlen:
11, 12, 13 ,....
Wenn ich frage: Welche natürlichen Zahlen sind größer gleich 10, dann sind das
10,11,12,...
Jede Zahl, die echt größer ist als 10, ist also auch größergleich 10, aber nicht jede Zahl, die größergleich 10 ist, ist auch echt größer als 10.
Induktionsschritt:
(1+x)^(n+1) = (1+x)^n * (1+x)
>= (Induktionsvoraussetzung)
(1+n*x)*(1+x) = 1+x+n*x+n*x*x >=
(da n*x*x >= 0 sein muss)
1+x+n*x = 1+(n+1)*x
ist aber etwas verwirrend, da echt größer nicht größer gleich ist, da echt größer heißt es ist insbesondere nicht gleich