Stimmt der Satz von Cavalieri auch bei einem kegel und einer halbkugel mit gleicher Höhe ?
Ich kann mir nicht vorstellen das ein Kegel und eine Halbkugel das selbe Volumen haben . Aber meinen Rechnungen zufolge ist das Volumen der beiden Körper identisch ( beide Radius 16.75cm |Höhe 33.5 cm ) wie kann das sein ?
4 Antworten
Ich würde das nochmal überprüfen, das kann so nicht sein.
Der radius ist in diesen Fällen aber eine unterschiedliche, höhenabhängige Variable
Was meinst du damit? Immer wenn die Höhe des Kegels doppelt so groß ist wie sein Radius bzw. der der Halbkugel, sind die Volumina identisch.
Kannst ja ne beliebige Höhe bzw. Radius einsetzen und die andere dazu passende Größe bestimmen, damit das gilt.
Ein Kegel hat das Volumenund eine Halbkugel
Gehen wir mal davon aus, dass Radius von Kegel und Halbkugel gleich sind, hab ich dasselbe Volumen, wenn giltalso die Höhe des Kegels doppelt so groß ist wie der Radius.
Genau das ist ja in deinem Beispiel so.
Irgendwas stimmt da in Deiner Überlegung nicht: Eine Halbkugel mit Radius 16,75 cm hat auch die Höhe 16,75 cm und nicht 33,5 cm!
Deine beiden Körper haben also nicht die selbe Höhe, der Kegel ist doppelt so hoch wie die Halbkugel - der Satz von Cavalieri ist also auf Deine Körper gar nicht anwendbar ...
- Eine Halbkugel hat das Volumen 2/3πr³h = (2πr³h)/3, in Deinem Fall also
(2*3,14...*16,75³)/3 = 9842,44...
- Ein Kegel hat das Volumen 1/3πr²h = (πr²h)/3, in Deinem Fall also
(3,14...*16,75²*33,5)/3 = 9842,44...
Deine beiden Körper haben also tatsächlich das gleiche Volumen - der Kegel ist aber eben doppelt so hoch wie die Halbkugel!
Es gilt also hier 2r = h, so dass die "2" und ein r aus dem "r³" aus der Halbkugelformel, die in der Kegelformel "fehlen", in diesem Fall genau durch das hinzugekommene "h" ausgeglichen werden.
Gleiche Höhe, gleicher Radius :
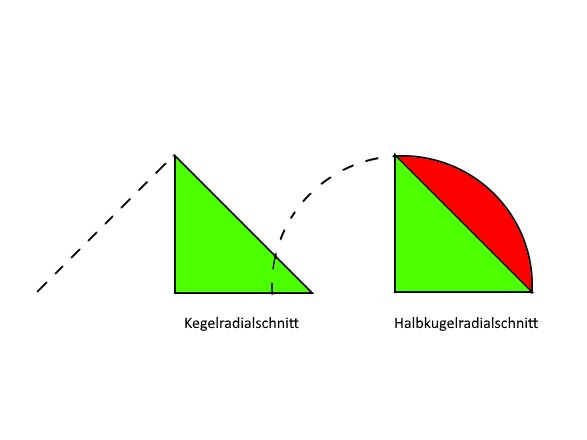
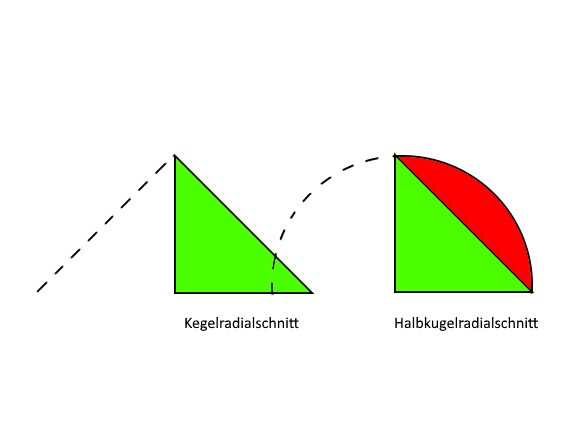
Doch. Immer wenn h=2r gilt ist das so.