Schwerpunkt eines Trapez (Formel)?
Ich hab ein rechtwinkliges Trapez. Ich muss die Entfernung des Schwerpunkt von der x-Achse herausfinden. Im Bild seht ihr alle Maße. Mit den Formeln aus dem Internet und von einer vorherigen frage kam die falsche Lösung raus. Ich hab mal S konstruiert, die Lösung ist 2,8 (nicht 2,5 wie alle vermuteten), ich brauche aber eine Formel dafür. Vielen Dank schon mal
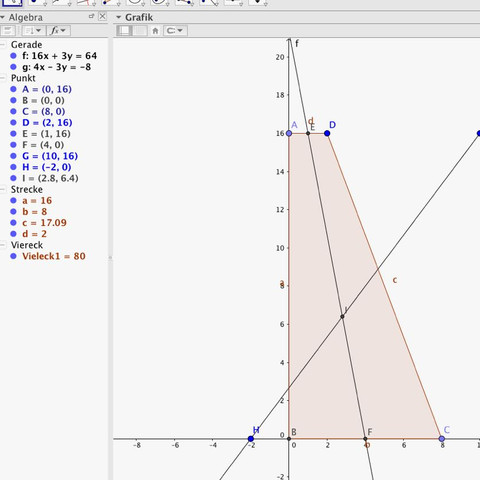
2 Antworten
Du kannst das Trapez in ein Rechteck und ein Dreieck aufteilen.
Der Schwerpunkt des Rechtecks ist sein Mittelpunkt, der Schwerpunkt des Dreiecks ist der Schnittpunkt der Seitenhalbierenden.
Der Ortsvektor des Schwerpunkts ist das "gewichtete" Mittel der Schwerpunkte der Teilflächen:
Wenn S1 der Schwerpunkt und F1 der Flächeninhalt der 1. Fläche ist und S2 der Schwerpunkt und F2 der Flächeninhalt der 2. Fläche, dann ist (Vektoren fett gesetzt):
S = F1 / (F1 + F2) * S1 + F2 / (F1 + F2) * S2
Hallo,
bei meiner vorgeschlagenen Lösung war ich davon ausgegangen, dass der Eckenschwerpunkt gefragt war, da dies nicht weiter präzisiert war.
Für diesen ist die hergeleitete Formel richtig.
Es gibt allerdings auch den Flächen- und den Kantenschwerpunkt.
Der Flächenschwerpunkt eines Vierecks stimmt mit dem Eckenschwerpunkt nur dann überein, wenn das Viereck nicht überschlagen und ein Parallelogramm ist.
Demnach fallen Ecken- und Flächenschwerpunkt bei deinem Trapez nicht zusammen, sondern sind verschieden.
Daraus schließe ich, dass du entweder den Flächen- oder den Kantenschwerpunkt meinst.
Hier ist ein Artikel (Mathe-Institut Uni München), der die drei verschiedenen Schwerpunkte eines Vierecks behandelt. Vielleicht kommst du damit weiter.
http://www.math.lmu.de/~fritsch/Viereckschwerpunkt
Gruß