Scheinbarer Widerspruch mit der Wegunabhängigkeit (Elektrisches Feld Plattenkondensator)?
Ich habe das E-Feld des Plattenkondensators noch um zwei Feldlinien erweitert:
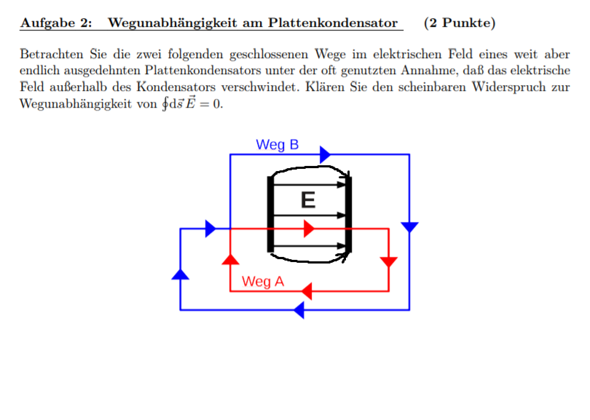
Also klar ist, außerhalb der Kondensatoren keine el. Feldstärke und auch, dass das Feld konservativ ist (Wegunabhängigkeit). Man sieht Weg B geht nicht durch den Kondensator, aber an ihm vorbei und eigentlich dürfte es noch den inhomogenen Teil des Feldes passieren oder doch nicht?
2 Antworten
Vorweg: Ich verstehe die Frage :)
Mein erster Impuls wäre der gleiche wie deiner, nämlich dass das Feld real nicht homogen ist. In der Skizze könnte man das auch in der Tat als Lösung annehmen und ich würde diese Vermutung auch in die Lösung einbeziehen, ich sehe aber zwei Probleme.
Das Feld ist außerhalb des Kondensators sicher wesentlich schwächer also wird das Linienintegral wohl dadurch nicht null, man könnte ja sogar den Kondensator in eine Metallkiste packe, sodass der äußere Pfad dann tatsächlich real keinem Feld ausgesetzt wäre (kannst du mir folgen?)
Alternativ könnte man den äußeren Pfad extrem ausdehnen, bis das Feld definitiv vernachlässigbar wäre.
Ich habe aber auch einen Lösungsvorschlag. Es geht vielleicht eher um das Feld in den Platten. Diese sind real ausgedehnt und die Bewerbung der Elektronen, erzeugt ein Gegenfeld, welches erst dafür sorgt, dass hinter den Platten kein Feld mehr besteht. Dieses Feld wird beim inneren Weg passiert, was das Integral immer rettet.
Sag bitte in jedem Fall Bescheid, was der Prof/Tutor als Musterlösung rausgibt bzw. ob meine Lösung passt :)
Also eine Musterlösung gab es nicht, aber es wurde gesagt, dass man die Aufgabe damit gelöst hat, wenn man darauf verweist, dass die Annahme, dass außerhalb des Kondensators das el. Feld verschwindet, falsch ist.
Das Linienintegral über den geschlossenen Weg ist Null. Da gibt's kein Wenn und Aber. Daher kann das Feld außen nicht Null sein.
Lies meine Antwort nochmal etwas beherzten.
Das Linienintegral ist null, in der Tat aber das Feld kann außerhalb durchaus verschwinden.
Es verschwindet außen einfach nicht ;-)
Bei deiner Argumentation kann ich nicht folgen...Du konstruierst irgendwas, um etwas zu retten, was nich rettbar ist. Das Feld in den Platten selbst ist Null. Deren Oberflächen sind Äquipotenzialflächen.
So sieht das Feld aus. Es IST "außen" nicht Null, nur eben deutlich schwächer als im Inneren.
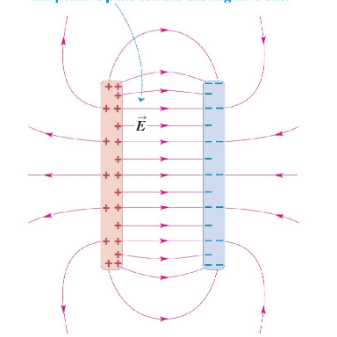
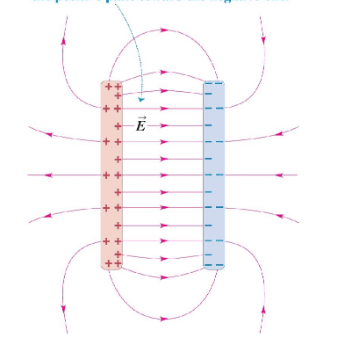
Zum Widerspruch:
Das Linienintegral muss laut Theorie, auf geschlossenen Wegen, immer null sein, insofern wäre das ein Widerspruch zur Theorie.
Der Grund ist die Energieerhaltung oder übergeordnet, dass es sich um ein konservatives Feld handelt.
Es ist aber eben nur ein scheinbarer Widerspruch, da in Wahrheit die Integrale eben doch null ergeben (siehe meine Antwort).
Aber was meinen die dann mit scheinbaren Widerspruch?
Dass oft gesagt wird, dass das Feld außen Null ist. Dann wäre das Integral über den roten Weg nicht Null - was aber nicht sein kann.
Ach so, okay, danke vielmals, dann hatte ich mit dem inhomogenen Teil ja den richtigen Riecher xD
Man kann sich das dadurch klarmachen, dass sich der Kondensator aus sehr vielen Dipolen zusammensetzt, deren Felder sich außerhalb des Kondensators nur in der Nähe der Platten und weit weg vom Rand der Platten tatsächlich annähernd aufheben.
Ja, kann ich :)
Michi meint freilich dazu:
Das harmoniert aber nicht ganz mit deiner Aussage, er sagt ganz klar, dass es Null ist.
Mach ich :)