Rechnen mit Fakultäten / Vollständige Induktion
Hallo,
ich arbeite mich gerade durch sämtliche Übungsaufgaben, die mir zwischen die Finger kommen. Es läuft auch alles gut, nur bei dieser hier weiß ich einfach gar nicht was ich machen soll, weil ich nicht weiß, wie ich mit der Fakultät rechne:
Summe von k=1 bis n .... (k+k!) soll (n+1)!-1 entsprechen (durch vollständige Induktion zeigen!)
Hab jetzt in meiner Formelsammlung nur gefunden, dass ich für (x+1)! auch x!(x+1) schreiben darf. Hilft das? Außerdem gilt doch: Fakultät vor Punkt- vor Strichrechnung ?!
Kann mir vielleicht irgendjemand noch irgendwas sinnvolles zur Fakultät sagen? Oder vielleicht die ganze Aufgabe rechnen? Es handelt sich nicht um Hausaufgaben, benotete Übungen oder ähnliches. In der Klausur werd ich sowas auch nicht machen müssen, aber es macht mich gerade wahnsinnig, dass alle anderen AUfgaben flutschen und die hier sich quer stellt.
Lieben Dank!
5 Antworten
Hat CatLikeThief,
könntest Du bitte die Aufgabe nochmal korrekt wiedergeben? Ich befürchte, Du hast hier eine falsche These aufgestellt. Schon im Fall n=1 und n=2 ist die Annahme falsch.
Der Induktionsschritt würde auch keinen Sinn machen. Generell gilt für die Fakultät die normale Multiplikationspriorität, da eine Fakultät ja nichts anderes ist als ein Produkt. Ich könnte Dir gerne bei der Aufgabe helfen, aber diese Aufgabe macht schlichtweg keinen Sinn. So kannst Du sie gar nicht lösen. Falsche Aufgabenstellung ;-)
Beste Grüße, Balu
So.. damit kann man jetzt arbeiten :-)
Also eigentlich hast du es schon fast dastehen. Ich gehe mal von deinem bisherigen Ergebnis aus (das bis jetzt vollkommen richtig ist):
(n+1)! - 1 + (n+1)(n+1)! |Jetzt einfach (n+1)! addieren und abziehen :-)
= (n+1)! - 1 + (n+1)(n+1)! + (n+1)! - (n+1)! |Jetzt ist (n+1)(n+1)! + (n+1)! = (n+2)(n+1)! und (n+1)! - (n+1)! = 0
= (n+2)(n+1)! -1 |Da a! * (a+1) = (a+1)! gilt
= (n+2)! - 1 = ((n+1) + 1)! -1
q.e.d.
Du musst hier also nur noch die Eigenschaften der Fakultät ausnutzen :-)
Ich hoffe, das war verständlich. Falls noch Fragen offen sind, einfach melden.
Beste Grüße, Balu
Du hast ja die Lösung im 2. Bild bereits gemacht!
Zuerst überprüfst du die Behauptung mit n=1 → dann mit der nächsten Zahl also n+1 → wenn das ach stimmt, dann gilt das natürlich auch für die übernächste - das nennt man vollständige Induktion - und somit auch für jede weitere Zahl, also für alle Zahlen (in diesem Fall natürlich für die Zahlenmenge ℕ = natürliche Zahlen, also zB nicht für Kommazahlen!)
Das ∑-Zeichen findest du natürlich nicht auf der Tastatur, aber es gibt verschiedenste Zeichensätze. Das ∑-Zeichen ist nichts anderes als der griechische Großbuchstabe Sigma, also ein großes S wie Summe. Ich verwende Linux, wo es ein eigenes Programm namens "Zeichentabelle" gibt. Sicherlich gibt es ähnliches auch im Windowsbereich, aber das verwende ich kaum (Eventuell in MS-Word/Excel nachschauen, da gibt es sicher spezielle Zeichensätze für Mathe). Viele Sonderzeichen liegen auch "unter" der Tastatur - einfach in einer reinen Textdatei ausprobieren. Bei mir finde ich u.a. Folgendes: AltGr+Tasten@ł€¶ŧ↝↓→øþ¨łĸħŋđðſæ, AltGR+Shift+Taste: Ωŝ€®Ŧ¥↑ıØÞŝ&˙ĦŊªÐẞÆ›‹©‚‘’º
Viel Spaß beim Durcharbeiten ☺☻
PS: Die Sonderzeichen (außer den Tastenbeispielen) sind aus dem Zeichensatz Courier New, den es meines Wissens auch in MS-Windows gibt.
Ne ne, ich muss noch zeigen, dass der linke Term dem rechten entspricht.
Ich muss also das, was ganz unten steht irgendwie umformen, damit es so aussieht wie der rechte Term der Induktionsbehauptung (IB). Da ich aber nicht weiß, wie ich da irgendwas umformen kann, komme ich nicht weiter.
Lieben Dank für die kleine Zeichensatz-Nachhilfe ;) Ist beim nächsten Mal sicher hilfreich
Direkter Beweis.
Man berechnet für k in N:
- ∆(k!) = (k+1)! – k! = (k+1)·k! – k! = k!·k
Daraus ergibt sich:
- ∑[k=1 bis n] k!·k
- = ∑[k=1 bis n] (k+1)! – k!
- = ∑[k=1 bis n] (k+1)! – ∑[k=1 bis n] k!
- = ∑[k=2 bis n+1] k! – ∑[k=1 bis n] k!
- = (n+1)! – 1!
- = (n+1)! – 1
W.z.z.w.
Summe von k = 1 bis n, also 1+2+3+4+...+n = 0,5 n (n + 1)
Produkt von k = 1 bis n, also 1 • 2 • 3 • 4 • ..... • n = n !
Den Rest verstehe ich nicht
Verständlich ;) Ohne das Summenzeichen ist es schon ein wenig wirr. Habe die Aufgabe abfotografiert. s. Antwort
Entschuldigung. Manchmal glaube ich, dass Leute die Mathe verstehen, jedes Zahlen-Buchstaben-Gewirr entziffern können. ;) Wieso hat meine Tastatur auch kein Summenzeichen? ;)
Also hier nochmal die Aufgabe :)
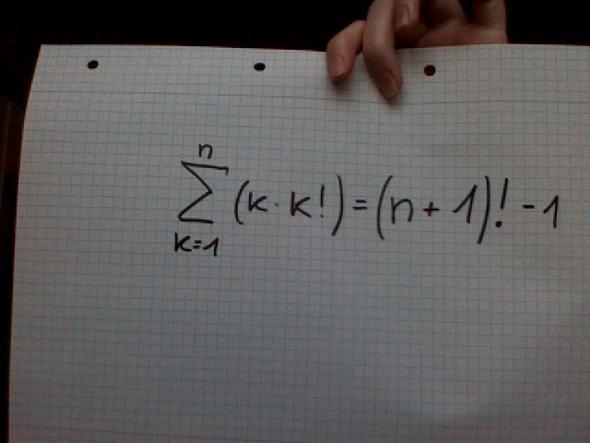
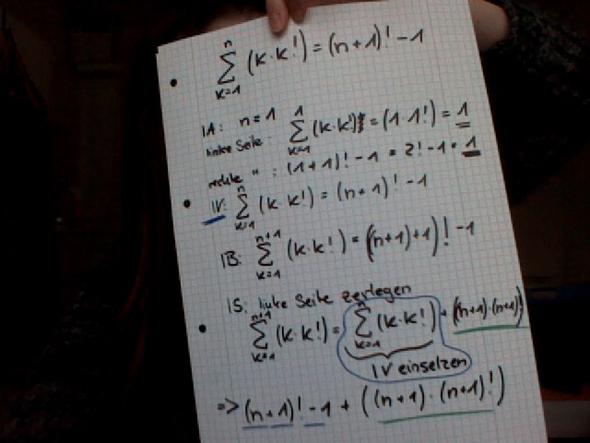
Entschuldige. Habe die Aufgabe groß aufgeschrieben und abfotografiert. s. Antwort