Mathe - Lösen dieser Aufgaben mit der vollständigen Induktion?
Hallo,
ich habe Probleme mit diesen 2 Aufgabem a und b, bei denen ich durch die Vollständige Induktion die Formeln herleiten muss.
Ich sitze da schon echt lange dran und habe echt keinen Plan wie ich das herleiten muss, damit auf beiden Seiten das selbe steht.
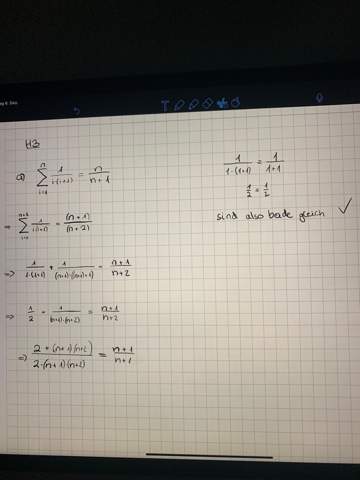
Für die Aufgabe a) habe ich einen ersten Ansatz, jedoch weiss ich nicht wie ich da weitermachen muss.
Wenn mir jemand mit beiden Aufgaben helfen könnte wäre ich echt sehr dankbar.
Danke schonmal im vorraus :)
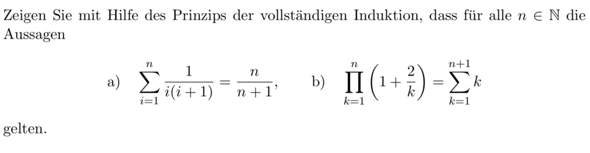
2 Antworten
Eigentlich ist das eine Teleskopsumme:
In der Summe bleibt daher nur über
und man kann diese sofort hinschreiben.
Aber auch der Induktionsschritt wird so geringfügig einfacher ;-)
Ich sehe deinen Ansatz noch nicht um ehrlich zu sein.
Wo ist der Induktionsanfang?
Und wo der Induktionsschritt?
Für den Schritt gilt foglendes:
Das sollte dir für den Start helfen. Vergleiche jetzt den Ausdruck mit der rechten Seite der Gleichung nämlich
Was musst du jetzt noch zeigen?
muss ich denn jetzt nicht noch in der rechten seite n+1 für n einsetzen?
Und rein logisch müsste ich doch nun beide seiten versuchen gleichzusetzen. Da komme ich aber nicht weiter
Das musst du nicht wegbekommen. Ja natürlich musst du auch rechts der Gleichung n+1 einsetzen. Dann steht da der Ausdruck den ich dir oben gepostet habe... = n+1/n+2
Wenn die Behauptung, die du durch die Induktion also beweisen willst stimmt, dann kannst du die Summe durch n/n+1 ersetzen. Der Beweis ist dann vollständig wenn du also zeigen kannst, daß n/n+1 + 1/((n+1)(n+2)) = n+1/n+2 ist
und wie genau kann ich das summenzeichen noch weg bekommen?