Problem mit Umschreiben eines Bruches
Hallo zusammen
Habe ein Bild von meinem "Problem" eingefügt. Und zwar bin ich mir im Allgemeinen nicht ganz sicher, wie man einen Bruch umschreibt.
Ich dachte immer, man stellt den Zähler vor den Nenner und ändert das Vorzeichen des Exponents im Nenner. Warum muss ich aber den Kehrwert von dem Bruch im Nenner nehmen?
Vielen Dank
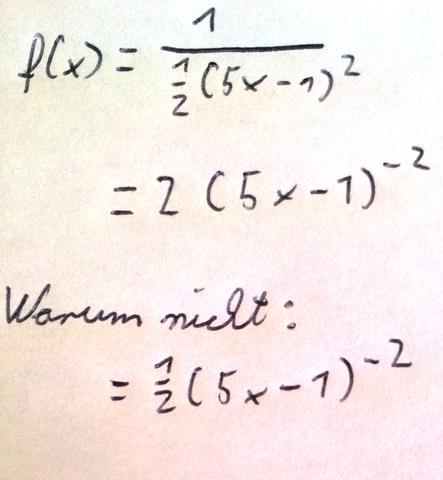
3 Antworten
Weil 1/(1/2 * (5x-1)²) = 1/(1/2) * (1/(5x-1)²)
(1/(5x-1)²) kannst du als (5x-1)^(-2) schreiben;
1/(1/2) = 1 * (2/1) = 2 (Durch einen Bruch zu dividieren ist das gleiche wie mit seinen Kehrbruch zu multiplizieren.
d.h. es steht dann 2 * (5x-1)^(-2) da.
Die erste Variante ist richtig. Die zweit nicht, weil 1/2 im Nenner steht und nicht im Zähler. Das ist ja ein Doppelbruch. Schau dir nochmal an, wie man die löst.
Noch etwas:
Im Zusammenhang mit dieser Aufgabe bekomme ich, wenn ich das Integral ausrechne:
-2 / (5*(5x - 1)) heraus.
Mein Lösungsbuch sagt mir, das könne man umschreiben in: 2 / (5* (1 - 5x))
Wieso denn das? Wird der ganze Bruch mit -1 multipliziert? Wieso wird dann die 5 vor der Klammer nicht auch negativ?
Ok , ich habs. Mit der Kettenregel, ist das einleuchtend.
Das mit dem * -1 macht keinen Sinn sehe ich gerade.