Nullstellen durch Ausklammern berechnen?
Wie müsste ich diese Aufgabe auklammern um die Gleichung Nullsetzten zu können, damit ich duch die PQ- Formel die Nullstellen herausbekomme?
f(x)=x^3-2x^2+x
Ich habe nichts gefunden wo es so erklärt wird, sodass ich es verstehe... Selbst Videos haben nicht geholfen.
Wäre für jede Hilfe dankbar :)
6 Antworten
Ausklammern bedeutet entweder einen gemeinsamen Faktor zu finden, der in jedem Glied der Funktion vorhanden ist, oder die clevere Anwendung der binomischen Formeln (praktisch "rückwärts")
In deinem Beispiel:
f(x) = x³ - 2x² + x
fällt als erstes auf, daß jeder Summand den Faktor x enthält. Der läßt sich ausklammern, die neue Gleichung lautet dann:
f(x) = x * (x² - 2x +1)
Wenn man jetzt den zweiten Faktor (x² - 2x +1) näher betrachtet, fällt einem die Ähnlichkeit zur (hoffentlich bekannten) 2. binomischen Formel auf:
(a-b)² = a² - 2ab - b²
also:
(x-1)² = x² - 2x +1
Die Gleichung kann man also umformen zu
f(x) = x * (x-1)²
Nullstellen findet man, wenn man weiß, daß die Multiplikation mit 0 immer 0 ergibt:
f(x) = 0 bedeutet also:
Entweder x=0 oder (x-1) = 0
Die Funktion hat also Nullstellen bei x = 0 und x = 1
Erklärung verstanden? Sonst frag nach!
Hey, also da du kein Absolutglied, also nur Werte mit der Variable x in deiner Funktion hast, kannst du die komplette Funktion in eine Klammer fassen und ein x ausklammern (x steht dann mit einer Multiplikation vor der Klammer).
So wird: aus x³ ---> x²
aus -2x² ---> -2x
aus x ---> 1
Das x , welches vor der Klammer steht ist dann immer die erste Nullstelle der Funktion bei x = 0.
Nun beachtest du dieses x vor der Klammer nicht weiter und in diesem Fall hier, befindet sich nun eine quadratische Funktion in der Klammer, auf die du nun die pq-Formel anwendest, um die anderen beiden Nullstellen zu berechnen (siehe Bild).
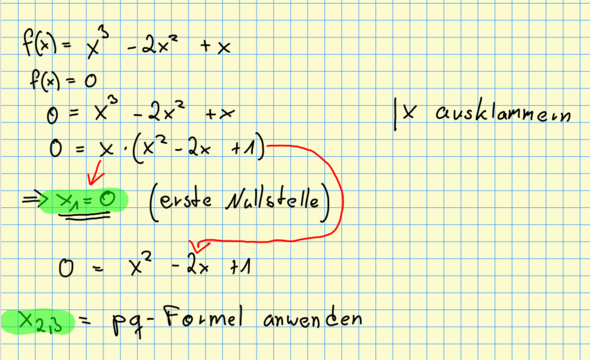
Du kannst in diesem Fall ein x ausklammern, damit nimmst du quasi ein x bei jedem Teil der Gleichung weg. Aus f(x)=x^3-2x^2+x wird dann f(x)=x*(x^2-2x+1). Um die Nullstellen nun zu bestimmen gilt f(x)=0.
Wenn du dies alles weißt musst du eigentlich nur noch wissen, dass ein Produkt gleich null ist, wenn einer der Faktoren null ist.
Also ist schon mal x=0. Die anderen Nullstellen kannst du jetzt einfach über die p-q-formel bestimmen.
Du klammerst lediglich ein x heraus.. In dem Fall also:
f(x)=x*(x^2-2x+1) = 0
Diese Konstellation sollte dir bekannt vorkommen. :)
Zu beachten ist, dass zusätzlich x=0 ist, da du es ausgeklammert hast.
lg
X(x^2-2x) also ist x=0 oder x^2-2x=0
X^2-2x kannst du dann normal in die pq Formel setzen