Normale einer Logarithmusfunktion?
Hey,
Ich habe die Funktion f(x)= ln(0,5x + 3). Die Nullstelle lautet -4 also ist y = 0. Der Punkt lautet also P(-4/0). Wie berechne ich nun die Gleichung der Normalen in der Nullstelle?
Soll ich diese Formel wie im Bild gezeigt nutzen? Wenn ja wie? Was ist z?
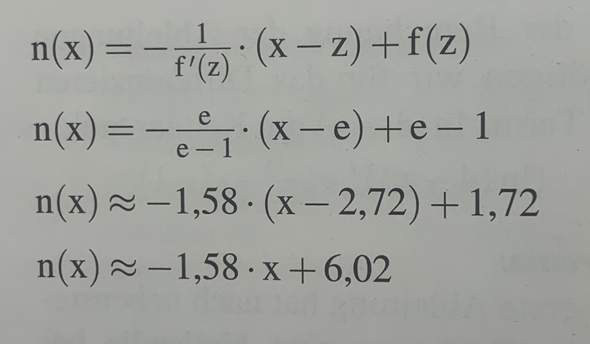
Danke! :)
4 Antworten
Normalengleichung yn=fn(x)=-1/f´(xo)*(x-xo)+f(xo)
xo=Stelle,wo die Normale an der Funktion f(x)=... liegen soll
Bei dir wurde ein anderer Buchstabe genommen → xo=z
f(x)=ln(0,5*x+3) Nullstelle xo=z=-4
abgeleitet f´(x)=1/(x+6)
f(xo)=f(-4)=ln(0,5*(-4)+3)=ln(1)=0
f´(xo)=f´(-4)=1/(-4+3)=-1
fn(x)=-1*(x-0)+0=-1*x
fn(x)=-1*x
Normale steht senkrecht auf der Tangente.
Vielleicht holst du dir erst die Steigung und schaust dann nach m_1 * m_2 = -1
Einen Punkt hast du dann, die Normalensteigung auch und so kommst dran.
Vorzeichenfehler. Die Steigung der Normalen muss -2 sein., den f'(-4)=0,5.
Man muss nur noch aus der Mittelstufe präsent haben
Geradengleichung t(x) = m x + n
Senkrechte Geraden m1 * m2 = -1
f(-4) = t(-4)
Das z in der Formel ist die x-Koordinate des Punktes, durch den die Normale gehen soll. In deinem Fall ist das die -4.
Beachte bitte, dass das Beispiel, welches du hier reingestellt hast, mit deiner Aufgaben nichts zu tun hat.
Bei den Schulmathematikern ist doch alles eine Formel!
Wenn Formeln Verständnis ersetzen läuft etwas im Unterricht falsch.
Erst Verständis, dann die Formel.
Die meisten wissen nicht mal woher oder was die PQ Formel ist, also ja, Verständnis ist generell nicht da.
Kann es sein das y = 2*x - 8 rauskommt?