(Mathe) Zimmermannsregel?
Hey,
also in Mathe hatten wir das Them Extremwertaufgaben mit Nebenbedingungen und da kam eine Aufgabe (die auch in der Klausur abgefragt werden soll) mit der Zimmermannsregel. Dabei ging es um die maximalste Tragfähigkeit von Balken. Diese Regel lautet ja: mache eine kreisförmigen Querschnittsfläche des Baumstammes, Durchmesser in drei teilen etc....
Ich verstehe nicht ganz wozu man diese "Regel" braucht...Also was bringt sie mir und was kann ich mit dem Ergebnis anfangen bzw. was bedeutet das Ergebnis für den Sachverhalt? Es hat ja was mit der max. Tragfähigkeit zu tun, aber was genau?...^^
Ich hoffe die Frage wirkt nicht arg dumm, jedoch verstehe ich den Sinn wirklich nicht...
1 Antwort
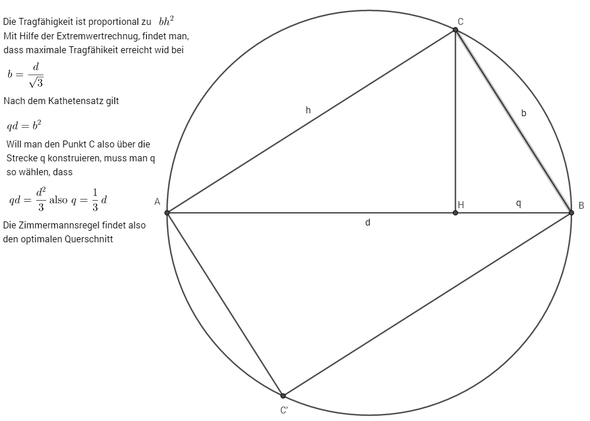
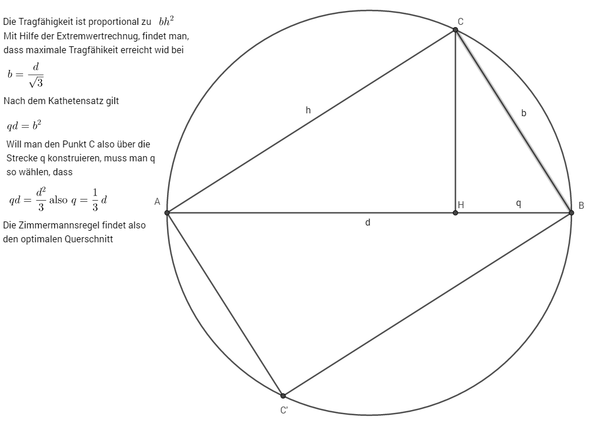
Typischerweise geht die Aufgabe so, dass man bei gegebenen Durchmesser d eines Baumstamms die Breite b und Höhe h eines einbeschriebenen Rechtecks bestimmen soll, so, dass die Tragfähigkeit T (die proportional zu b*h^2 ist) maximal wird. Es gibt ein k, so dass
T = k*b*h^2 = k*b*(d^2-b^2)
Leitet man das nach b ab und setzt Null, so kommt heraus, das maximale Tragfähigkeit bei
d
b = ------
\/ 3
gegeben ist. Ein Zimmermann müßte also den Durchmesser durch Wurzel(3) teilen, um die Breite anreißen zu können. Stattdessen kontruiert er die Breite, indem er ein Drittel des Durchmessers anzeichnet und von dort senkrecht nach oben geht.
Die Frage ist nun, wie weit der Zimmermann von der optimalen Lösung entfernt ist. Mithilfe des Kathetensatzes (z.B) kann man einsehen, dass die Konstruktion des Zimmermanns tatsächlich das Optimum trifft.
ok, vielen vielen Dank. Das ergibt sehr viel Sinn^^. Aber nur damit ich mir sicher bin; mit max. Tragfähigkeit ist schon gemeint wie man den Holzbalken schneiden muss damit er optimal etwas tragen kann, also weder zu dünn noch zu dick dafür ist und nicht brechen kann oder so....?Dann nochmal vielen Dank!