Kann mir jemand dabei helfen diese Aufgabe zu lösen?
Hallo,
ich habe hier eine Aufgabe, welche ich nicht lösen kann.
Die Aufgabe lautet:
Eine 4,5 m lange Leiter darf nur mit einem Neigungswinkel zwischen 65° und 75° an eine Wand gelehnt werden. Erstelle eine geeignete Planskizze.
a) Wie weit muss die Leiter mindestens und wie weit darf sie höchstens von der Wand entfernt aufgestellt werden?
b) Eine Leiter reicht bei einem Neigungswinkel von 70° bis in die Höhe von 3,5 m. Berechne die Länge der Leiter.
2 Antworten
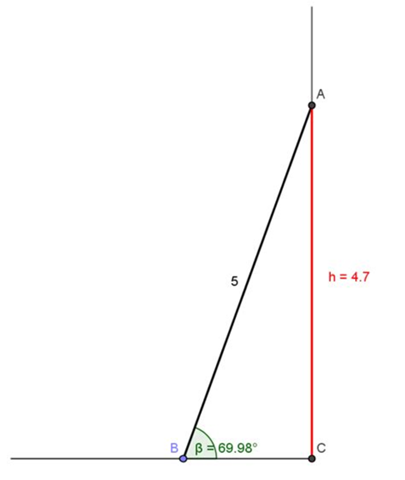
Erstelle eine Skizze. Zeichne ein rechtwinkliges Dreieck. Die Leiter ist dabei die Hypothenuse, die Ankathete zu dem Neigungswinkel ist die Entfernung von der Wand bis zu dem Punkt, wo die Leiter steht und die Gegenkathete ist die Höhe vom Boden bis zu dem Punkt, wo die Leiter an der Wand anlehnt.
a) Die Entfernungen von der Wand sind die Längen der Ankatheten zu den möglichen Neigungswinkel, also 4,5m ⋅ cos(75°) bis 4,5m ⋅ cos(65°).
b) Die Höhe ist Länge ⋅ sin(70°) = 3,5m.
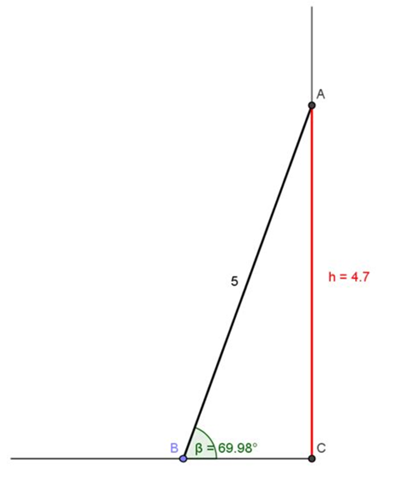
AB ist die Leiter 4.5 m lang.
.
Gesucht BC
.
Gegeben Hypo und Ankathete >>> cos
.
Cos(65) = BC/4.5
.
.
b)
.
sin(70) = 3.5/Länge