Mathe Mittelpunkt eines Vektors Aufgabe?
Hey Leute,
Wir machen gerade das Thema Vektoren in Mathe, speziell den Mittelpunkt einer Strecke. Ich weiß, dass die Formel
1/2 * (A+B) = M
ist, um den Mittelpunkt rauszubekommen. Nun muss ich in einem Parallelogramm die Punkte C und D berechnen mithilfe von Punkt A, B und dem Mittelpinkt der Diagonale. Im Bild unten seht ihr, wie weit ich schon bin.
Ich weiß nicht, wie ich D berechnen soll. Kann mir jemand weiterhelfen?
Dankesehr!!!
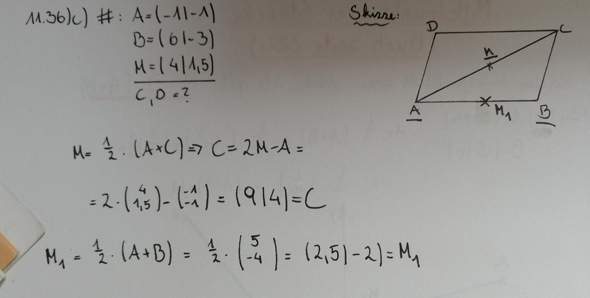
1 Antwort
Mittelpunkt der Diagonale:
M_diag = 1/2 (A + C)
Diese Gleichung kannst du nach C umstellen.
Bei einem Parallelogramm sind gegenüberliegende Seiten parallel und gleichlang, werden also durch denselben Vektor beschrieben. D. h.
B - A = C - D
C - B = D - A
Diese Gleichungen kannst du nach D umstellen und obiges Ergebnis für C einsetzen.
-----
Oder du nutzt, dass die Diagonalen eines Parallelogramms sich gegenseitig halbieren. Dann ist der Mittelpunkt der einen Diagonalen auch der Mittelpunkt der anderen, d. h.
M_diag = 1/2 (B + D)
Da M_D und B gegeben sind, kannst du hieraus D berechnen.
Vielen vielen Dank, hat mir extrem weitergeholfen!!! :D
Selten eine so genaue und ausführliche Antwort bekommen, die so gut erklärt und verständlich ist, vielen Dank!
L G