Mathe Maximalen Gewinn berechnen?
Ich habe alles richtig berechnet, aber frage mich jetzt was nun eig der Maximale Gewinn ist.. xD
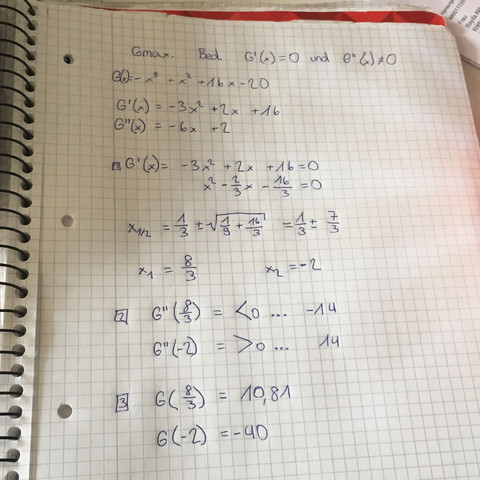
4 Antworten
Du hast es doch unten stehen...
Ein Maximum liegt vor, wenn G'(x)=0 und G''(x)<0 ist und das ist bei Dir bei x=8/3 der Fall und der Funktionswert bei x=8/3 ist G(8/3)=10,81. Das ist das Maximum (für x<0 wirst Du ab einer bestimmten Stelle höhere Funktionswerte erhalten, aber ich denke mal, dass die Funktion für positive x definiert sein soll.)
G(-2) hättest Du demnach gar nicht erst ermitteln brauchen; erstens wird x=-2 nicht zur Definitionsmenge gehören und zweitens ist G''(-2)>0, d. h. an dieser Stelle ist ein lokales Minimum.
(Anmerkung: Du solltest die Ergebnisse Deiner Berechnung der 2. Ableitung vorne hinschreiben, nicht irgendwo ans Ende hinter 3 Punkten, also z. B. G''(8/3)=-14 <0 => Maximum bei x=8/3)...)
aha, eigenartig; von der Logik her schreibe ich doch zuerst das errechnete Ergebnis hin und dann, ob dieses Ergebnis kleiner oder größer Null ist. Aber gut, wenn dieser Lehrer es unbedingt so will...
Da muss schon ein bisschen mehr kommen als nur ein mieses Handyfoto.
Da Abkürzungen mitnichten vereinheitlicht sind, können nicht alle was mit G' oder G'' anfangen.
Was ist die Gesamtkostenfunktion?
Wie hoch ist der Verkaufspreis?
Gibt es eine Nachfragekurve, oder soll die hier vernachlässigt werden?
(8/3) ist die Hochstelle, dann ist G (8/3) das Maximum
10,81 wäre jetzt der max. Gewinn.
Zu der Anmerkung, unser Lehrer will dass wir es so machen.