Mathe Hilfe drei Lineare Gleichungen mir 3 Variablen?
Hallo, ich verstehe aufgabe f) nicht könnte jemand die für mich lösen und erklären schrittweise, wie er vorgegangen ist!
wäre super lieb, danke
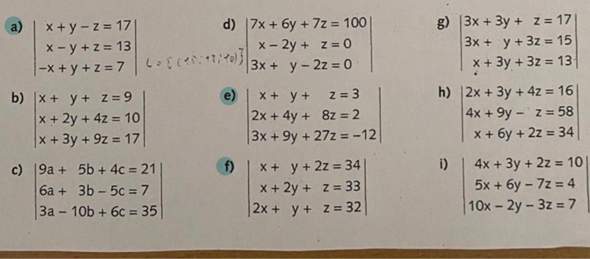
5 Antworten
a) I x + y - z = 17
II x - y + z = 13
III -x + y + z = 7
Für drei Unbekannte muss man erst einmal
aus je zwei Zeilen eine machen.
Gebraucht werden eigentlich zwei Zeilen.
Man muss sich entscheiden, welche man
eliminiert. Ich nehme z.
Das geht gut bei z, weil die
Vorzeichen schon unterschiedlich sind.
Sonst hätte ich nochmal multiplizieren
müssen. Daher
I+II 2x = 30 | /2
I+III 2y = 24 | /2
Schöner Zufall! Meistens gibt es
2 Gleichungen mit 2 Unbekannten.
Hier sofort weiter:
I+II x = 15
I+III y = 12
Es fehlt noch z. Dafür nehme ich
Gleichung II (ist aber egal):
15 - 12 + z = 13
3 + z = 13 | -3
z = 10
Hinweis:
Bei 3 oder mehr Unbekannten ist das
Additionsverfahren immer das beste!
f)
Bei der 1. Gleichung nichts tun.
II und III mit (-2) multiplizierem,
und zwar alle Terme in den Gleichungen!
Dann ist z weg.
Also wenn du die andern verstanden hast, verstehst du auch Aufgabe f.
Es ist ja immer das gleiche "Kochrezept" mit den Matrizen.
Ab einem gewissen Stadium darfst du das sicher auch mit dem Taschenrechner machen; ich verwende dazu immer ein selbstgeschriebenes Programm auf dem "TI-82_stats".
ob man zuerst x y oder z verschwinden lässt , kommt aufs eigene Gefühl für die Zahlen an .
Man braucht hier auf jeden Fall immer zwei Aktionen , damit man eine Variable wegbekommt . Zwei Variablen zu gleich sind nicht möglich.
Mein Vorschlag ( geht eher zufälligerweise recht schnell, das war keine Planung )
.
I - II
x-x + y-2y + 2z-z = 34-33
0 -y + z = 1....................(4)
.
2 mal I - III
2x-2x + 2y-y + 4z-z = 68-32
0 + y + 3z = 36...............(5)
.
(4) und (5) addieren
-y+y +z+3z = 1+36
0 + 4z = 37
z = 37/4
.
Mit schnell war gemeint, dass (4) und (5) schon so vorliegen, dass man gleich z eleminieren kann.
Es gibt da viele Möglichkeiten das zu lösen. Gleichsetzungsverfahren, Additionsverfahren, Einsetzungverfahren. Beherrscht du alle drei?

Quelle

Für das Lösen von LGS gibts diverse unterschiedliche Verfahren. Welche habt ihr denn schon drangenommmen bzw. welches Verfahren soll da geübt werden?