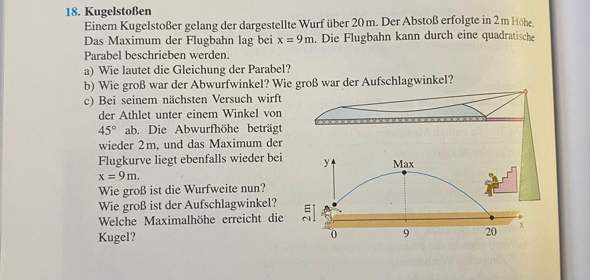
kann mir jemand bei den Aufgaben b und c erklären, was man da machen muss?

.

Answer 1

[evtldocha]

Scheitelpunkt liegt genau in der Mitte der Nullstellen. Nach rechts zur Nullstelle sind es vom x-Wert des Scheitelpunkts (20 - 9) m = 11 m. Also müssen es auf der andere Seite ebenfalls 11 m bis zur Nullstelle sein. Daher: $f\left(x\right)=a\cdot\left(x+2\right)\cdot\left(x-20\right)$

Den Streckfaktor "a" kann man aus der Abwurfhöhe 2 m bei x=0 bestimmen: $f\left(0\right)=a\cdot\left(0+2\right)\cdot\left(0-20\right)=2\ \to a=\ \frac{2}{\left(-40\right)}=-\ \frac{1}{20}$

Damit $f\left(x\right)=-\frac{1}{20}\cdot\left(x+2\right)\cdot\left(x-20\right)=-\frac{1}{20}x^2+\frac{9}{10}x+2$

Aufgabe b)

Abwurfwinkel: tan(α) = f'(0)
Aufschlagwinkel: tan(α) = f'(20)

Aufgabe c) Das ist dann eine Steckbriefaufgabe mit:

$\left(1\right)\ f\left(0\right)=2$ $\left(2\right)\ f'\left(0\right)\ =\ 1\ \ \left(=\tan\left(45°\right)\right)$ $\left(3\right)\ f'\left(9\right)=0$

Answer 2

[Tannibi]

Du hast die Gleichung der Parabel. Berechne die
Ableitung und deren Werte bei 0 und 20 m.
Das ist die Steigung der Parabel und der Tangens
des Winkels, also arctan der Steigung = Winkel.

Für c) musst du eine neue Parabel berechnen, dann wie bei b).